Hallo Alissa,
Wie gebe ich die Ebene E durch die Geraden g und h in Normalenform an?
Voraussetzung ist natürlich, dass \(g\) und \(h\) in einer Ebene liegen. Das ist hier aber der Fall. Berechne einen Normalenvektor aus dem Kreuzprodukt der Richtungsvektoren der Geraden und normiere ihn. D.h. teile den Vektor durch seine Länge, so dass der Normalenvektor \(\vec n\) die Länge 1 bekommt:
$$\begin{pmatrix}-3\\ 1\\ 1\end{pmatrix} \times \begin{pmatrix}1\\ -1\\ 1\end{pmatrix} = \begin{pmatrix}2\\ 4\\ 2\end{pmatrix} \quad \to \vec n = \frac 1{\sqrt 6} \begin{pmatrix}1\\ 2\\ 1\end{pmatrix}$$
Die Multiplikation mit einem der Stützpunkte der Geraden liefert dann die rechte Seite der Hesseschen Normalform der Ebene:
$$E: \quad \vec n \cdot \vec x = \vec n \cdot \begin{pmatrix}4\\ 2\\ 2\end{pmatrix} \\ E: \quad \frac 1{\sqrt 6} \begin{pmatrix}1\\ 2\\ 1\end{pmatrix} \vec x = \frac {10}{\sqrt 6}$$
Wie kann ich überprüfen, ob P in der Ebene E liegt? (ohne Rechnung)
ohne Rechnung mit einem Bild in 3D
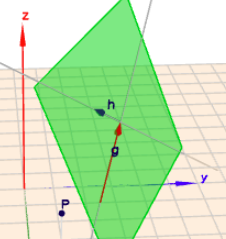
Wenn Du auf das Bild klickst, kannst Du die Szene rotieren und man sieht dann, dass \(P\) nicht in \(E\) liegt.
Ansonsten setze \(P\) in die linke Seite der Ebenen-Gleichung ein:
$$\frac 1{\sqrt 6} \begin{pmatrix}1\\ 2\\ 1\end{pmatrix} \cdot \begin{pmatrix}3\\ 1\\ 1\end{pmatrix} = \sqrt 6$$Die Differenz \(d\) zur rechten Seite von \(E\) liefert den Abstand zur Ebene$$d = \left|\sqrt 6 - \frac {10}{\sqrt 6} \right| = \frac 4{\sqrt 6} \approx 1,63$$
und da dieser \(\ne 0\) ist, liegt \(P\) nicht in \(E\).
Die Gerade g soll in der Ebene E um 90° gedreht werden.
Dann müsste noch ein Punkt gegeben sein, um den gedreht wird. Ich nehme mal den Stützpunkt von \(P\). Die neue Richtung kann man über das Kreuzprodukt mit \(\vec n\) berechnen:$$ \vec n \times \begin{pmatrix}-3\\ 1\\ 1\end{pmatrix} = \frac 1{\sqrt 6} \begin{pmatrix}1\\ -4\\ 7\end{pmatrix}$$den Faktor \(1/\sqrt 6\) kann man beim Richtungsvektor weg lassen. Das sieht dann im Bild so aus
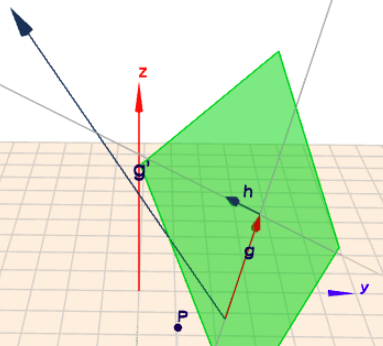
$$g': \quad \vec x = \begin{pmatrix}4\\ 2\\ 2\end{pmatrix} + t\cdot \begin{pmatrix}1\\ -4\\ 7\end{pmatrix}$$