Wie begründe ich anhand der folgenden Abbildung, dass der Graph der Funktion folgende Eigenschaften erfüllt?
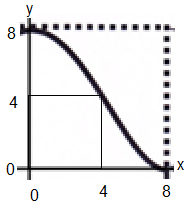
f´ (0)=0 , an der Stelle x=0 hat der Graph eine waagerechte Tangente
f´´(4)=0 , an der Stelle x=4 ist die Steigung des Graphen lokal extrem.
f´´(0)<0 , an der Stelle x=0 hat der Graph eine Rechtskurve.
f(-8)=0 Der Punkt (8|0) liegt auf dem Graphen.
Wie begründe ich, dass die ganzrationale Funktion mindestens den Grad 4 haben muss?
Da Symmetrie zur y-Achse vorliegt, muss der Grad gerade sein, da ein Wendepunkt vorliegt muss der Grad ≥3 sein.