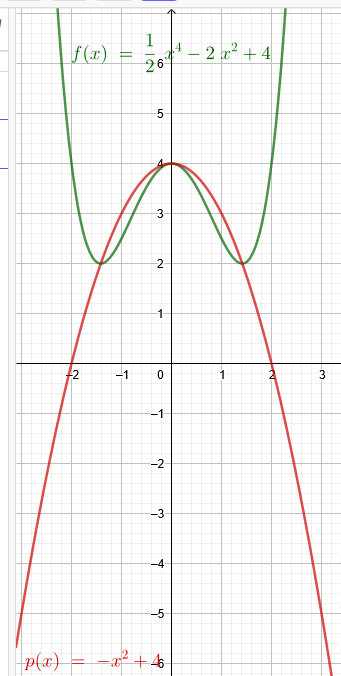
a.) Unter welchem Winkel schneidet der Graph von f(x) und f(0) überein?
f(x)=\( \frac{1}{2} \)x^4-2x^2+4
f´(x)=2x^3-4x
f´(0)=0 Der Graph schneidet die y-Achse unter einem Winkel von 90°
b.) Eine nach unten geöffnete Parabel, deren Scheitel im Hochpunkt von f liegt, soll durch die beiden Tiefpunkte von f gehen. Bestimmen sie die Gleichung
f´(x)=2x^3-4x
2x^3-4x=0
x*(2x^2-4)=0
x₁=0
x₂=\( \sqrt{2} \)
x₃=-\( \sqrt{2} \)
Art der Extremwerte:
f´´(x)=6x^2-4
f´´(0)= - 4 < 0 Hochpunkt
f´´(\( \sqrt{2} \))=6*2-4=8>0 Minimum
f´´(-\( \sqrt{2} \))=6*2-4=8>0 Minimum
Scheitelpunkt der Parabel: S(0|f(0))->-> S(0|4)
p(x)=a*x^2+4
p(\( \sqrt{2} \))=2a+4
f(\( \sqrt{2} \))->->\( \frac{1}{2} \)*4-2*2+4=2-4+4=2
2a+4=2->->a=-1
p(x)=-*x^2+4