Aloha :)
Wir untersuchen die Funktion$$f(x)=\frac{2-x^2}{x^3}+e^x=\frac{2}{x^3}-\frac{1}{x}+e^x=2x^{-3}-\frac{1}{x}+e^x$$
Zur Bestimmung der gesuchten Fläche \(A\) benötigen wir eine Stammfunktion$$F(x)=e^x-\ln|x|-\frac{1}{x^2}$$
Weiter zeigt uns das Schaubild im Intervall \([-5|-0,5]\)
~plot~ (2-x^2)/x^3+e^x ; x=-5; x=-0,5 ; {-1,214|0} ; [[-6|0|-4|0,5]] ~plot~
dass ein Teil der eingeschlossenen Fläche oberhalb der \(x\)-Achse verläuft und ein Teil der eingeschlossenen Fläche unterhalb der \(x\)-Achse. Zur Berechnung der gesuchten Fläche \(A\) benötigen wir die Nullstelle \(x_N\) der Funktion \(f\) im betrachteten Intervall \([-5|-0,5]\). Diese Nullstelle \(x_N\) ist nur numerisch zu berechnen. Wir wählen Newton-Verfahren:$$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}=x_n-\frac{\frac{2}{x^3}-\frac{1}{x}+e^x}{-\frac{6}{x^4}+\frac{1}{x^2}+e^x}\quad;\quad x_0=-1$$
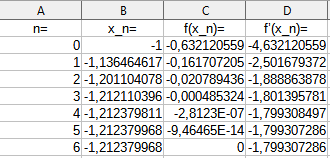
Die Nullstelle liegt also bei \(x_N=-1,21237996755972\).
Damit können wir die gesuchte Fläche \(A\) bestimmen:
$$A=\int\limits_{-5}^{x_N}f(x)dx-\!\!\!\int\limits_{x_N}^{-0,5}f(x)dx=\left(\,F(x_N)-F(-5)\,\right)-\left(\,F(-0,5)-F(x_N)\,\right)$$$$\phantom{A}=2F(x_N)-F(-5)-F(-0,5)$$$$\phantom{A}=2\cdot(-0,575431422241778)-(-1,64269996543502)-(-2,70032215972742)$$$$\phantom{A}=3,19215928067888$$