f ( x) =x^3 + bx^2+cx + d
d ist der y-Achsenabschnitt
Eine Änderung von d würde die Kurve nach
oben oder unten verschieben.
Würde aber an Steigungen / Krümmungen nichts
ändern
a) genau einen Hoch- und genau einen Tiefpunkt besitzt,
f ´ ( x ) = 3 * x^2 + 2 * b * x + c
Stellen mit waagerechter Tangente
3 * x^2 + 2 * b * x + c = 0
x gleich
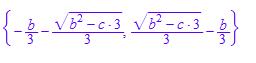
Es ergeben sich 2 Lösungen
Falls √ [ ( b^2 - 3*c ) / 3 ] = 0 ist reduziert
sich die Lösung auf -b/3
√ [ ( b^2 - 3*c ) / 3 ] = 0
( b^2 - 3*c ) / 3 = 0
b = ± √ ( 3c )
oder
c = b^2 / 3
Für diese Werte ist EINE waagerechte Tangente
Stelle vorhanden
Beispiel
b = 2
b^2 / 3 = 4/3
c = 4/3
x = -b/3 = -2/3
Krümmung
f ´´ ( x ) = 6 * x + 2* b
f ´´ ( -b/3 ) = 6 * (- b/3 )+ 2* b
f ´´ ( -2/3 ) = 6 * (- 2/3 ) + 2* 2
f ´´ ( -2/3 ) = 0
Die Krümmung ist 0 = Sattelpunkt
Hoffentlich stimmt das alles
Bitte nachprüfen und nachfragen.