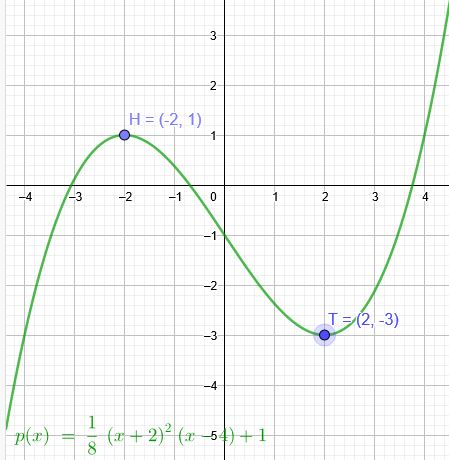
a) Der Graph 1 (3. Grad) hat in \(H(-2|1)\) einen Hochpunkt und in \(T(2|-3)\) einen Tiefpunkt.
Ich verschiebe um eine Einheit nach unten:
\(H(-2|1)\)→ \(H´(-2|0)\) Hier ist nun eine doppelte Nullstelle:
\(f(x)=a(x+2)^2(x-N)\)
\(T(2|-3)\)→ \(T´(2|-4)\)
\(f(2)=16a(2-N)\)
\(16a(2-N)=-4\) → \(4a(N-2)=1\) → \(a=\frac{1}{4N-8}\)
\(f(x)=\frac{1}{4N-8}[(x+2)^2(x-N)]\)
Tiefpunkteigenschaft:
\(f´(x)=\frac{1}{4N-8}[(2x+4)(x-N)+(x+2)^2]\)
\(f´(2)=\frac{1}{4N-8}[(4+4)(2-N)+(2+2)^2]=\frac{1}{4N-8}[32-8N]\)
Aufgabe b) kann auch auf diese Art bestimmt werden.
\(\frac{1}{4N-8}[32-8N]=0\) \(N=4\) \(a=\frac{1}{8}\)
\(f(x)=\frac{1}{8}(x+2)^2(x-4)\)
Nun eine Einheit nach oben:
\(p(x)=\frac{1}{8}(x+2)^2(x-4)+1\)