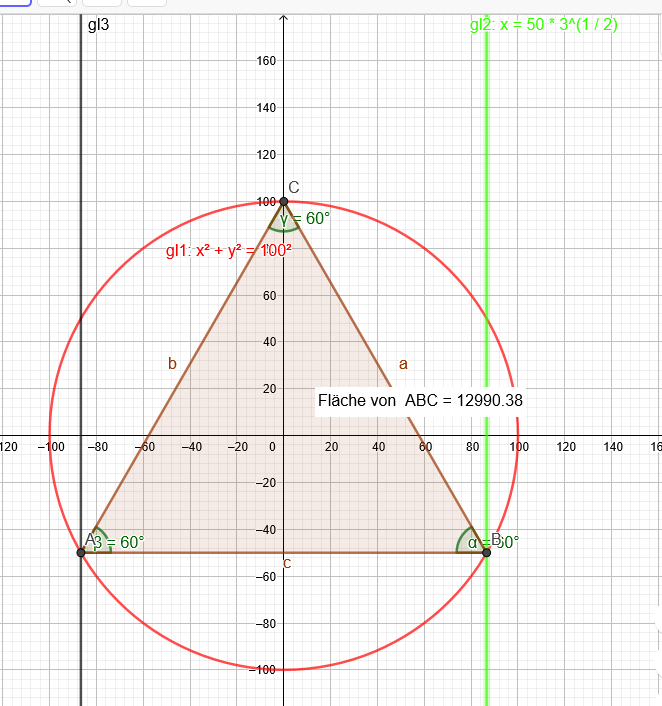
Du hast Recht, da fehlt unter der Wurzel das Quadrat bei der 100. Bei der Zeichnung habe ich noch daran gedacht.
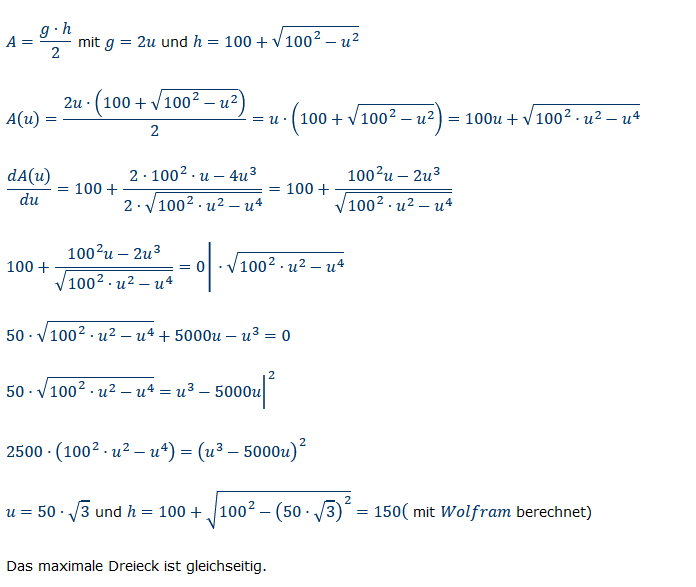
Text erkannt:
\( A=\frac{g \cdot h}{2} \) mit \( g=2 u \) und \( h=100+\sqrt{100^{2}-u^{2}} \)
\( A(u)=\frac{2 u \cdot\left(100+\sqrt{100^{2}-u^{2}}\right)}{2}=u \cdot\left(100+\sqrt{100^{2}-u^{2}}\right)=100 u+\sqrt{100^{2} \cdot u^{2}-u^{4}} \)
\( \frac{d A(u)}{d u}=100+\frac{2 \cdot 100^{2} \cdot u-4 u^{3}}{2 \cdot \sqrt{100^{2} \cdot u^{2}-u^{4}}}=100+\frac{100^{2} u-2 u^{3}}{\sqrt{100^{2} \cdot u^{2}-u^{4}}} \)
\( 100+\frac{100^{2} u-2 u^{3}}{\sqrt{100^{2} \cdot u^{2}-u^{4}}}=0 \mid \cdot \sqrt{100^{2} \cdot u^{2}-u^{4}} \)
\( 50 \cdot \sqrt{100^{2} \cdot u^{2}-u^{4}}+5000 u-u^{3}=0 \)
\( 50 \cdot \sqrt{100^{2} \cdot u^{2}-u^{4}}=u^{3}-\left.5000 u\right|^{2} \)
\( 2500 \cdot\left(100^{2} \cdot u^{2}-u^{4}\right)=\left(u^{3}-5000 u\right)^{2} \)
\( u=50 \cdot \sqrt{3} \) und \( h=100+\sqrt{100^{2}-(50 \cdot \sqrt{3})^{2}}=150 \) ( mit Wolfram berechnet)
Das maximale Dreieck ist gleichseitig.