Eine Gerade g hat die Steigung m=2 und geht durch den Punkt P(8/12).
g: y = mx + b = 2x + b
12 = 2*8 + b
b = -4
Die Geradengleichung lautet also
y = 2x - 4
Die Gerade sieht so aus:
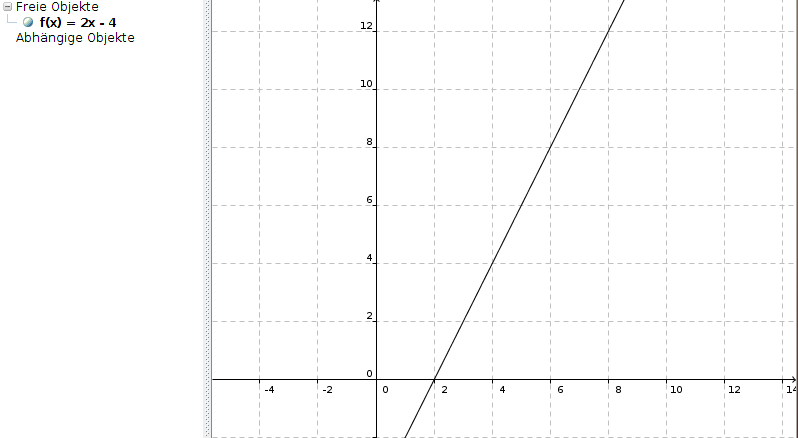
Schnittpunkt mit der x-Achse:
Wir setzen y = 0
0 = 2x - 4
4 = 2x
x = 2
Schnittpunkt mit x-Achse (2|0)
Schnittpunkt mit der y-Achse:
Wir setzen x = 0
y = 2 * 0 - 4 = -4
Schnittpunkt mit der y-Achse (0|-4)
Welchen Flächeninhalt hat das Dreieck, das die Gerade mit den beiden Koordinatenachsen bildet?
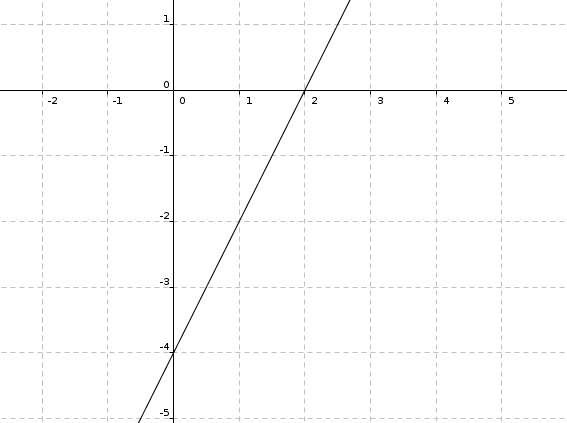
Flächeninhalt eines Dreicks = Breite * Höhe / 2, also hier
A = 2 * 4 / 2 = 4
Besten Gruß