Aufgabe: Stückweise definierte Funktion - Erlösfunktion.
Hallo allerseits :), ich hoffe ihr könnt mir helfen.
"Monopolistische Konkurrenz: Für ein Unternehmen unter monopolistischer Konkurrenz existieren folgende Zusammenhänge zwischen der abgesetzten Menge und dem Preis: Der maximale Verkaufspreis liegt bei 30€/Stück. Bei einem Preis von 25€/Stück werden 10 Stück abgesetzt. Eine weitere Senkung des Preises auf 10€/Stück führt zu einem Absatz von 20 Stück. Die größte absetzbare Menge bei einem Preis von 0€/Stück liegt bei 40 Stück."
(a) Geben Sie das abschnittsweise lineare Modell der Preis-Absatz-Funktion an.
(b) Bestimmen Sie den Absatz bei einem Preis von 24€/Stück.
(c) Wie hoch ist der Stückpreis, wenn man einen Absatz von 30 Stück erzielt.
(d) Erstellen Sie aus der Nachfragefunktion die zugehörige Erlösfunktion.
Problem/Ansatz:
(e) Bestimmen Sie den Absatz bei einem Erlös von 266.66€ und den zugehörigen Preis.
a,b,c,d ist für mich verständlich, doch bei der Erlösfunktion komm ich einfach nicht weiter.
Die Lösung sollte p = 20€/Stück und Absatz 13.33 Stück sein, doch ich weiß nicht wie ich das ausrechnen soll.
vielen dank im voraus !!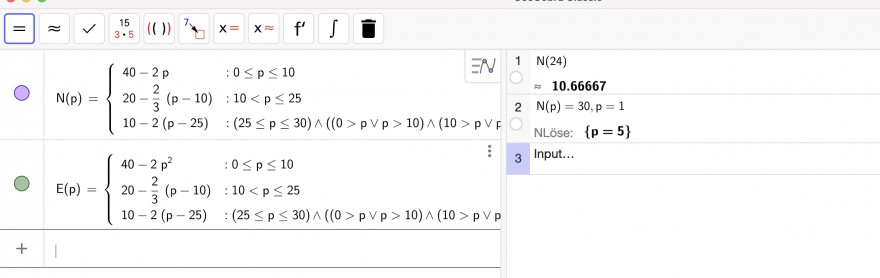
Text erkannt:
\( =\approx \sim \mid \begin{array}{c}15 \\ 3 \cdot 5\end{array} \)
\( N(p)=\left\{\begin{array}{llll}40-2 p & : 0 \leq p \leq 10 & \text { INd } & 1 & \text { N(24) } \\ 20-\frac{2}{3}(p-10) & : 10<p \leq 25 & & \approx 10.66667 \\ 10-2(p-25) & :(25 \leq p \leq 30) \wedge\left((0>p \vee p>10) \wedge\left(10>p \vee_{F}\right.\right. & 2 & N(p)=30, p=1 \\ & & & \text { NLöse: }\{\mathbf{p}=5\}\end{array}\right. \)
\( E(p)=\left\{\begin{array}{ll}40-2 p^{2} & : 0 \leq p \leq 10 \\ 20-\frac{2}{3}(p-10) & : 10<p \leq 25 \\ 10-2(p-25) & :(25 \leq p \leq 30) \wedge((0>p \vee p>10) \wedge(10>p \vee p\end{array}\right. \)
