Kostenfunktion: K(x) = 1/4·x^2 - 1/2·x + 5
Gegeben ist im Intervall [0; 15] eine Kostenfunktion K mit K(x) = 1/4·x^2 - 1/2·x + 5 und eine Erlösfunktion mit E(x) = 3·x
a) Zeichnen sie die zu K und E gehörigen Graphen und geben sie die Fixkosten an.
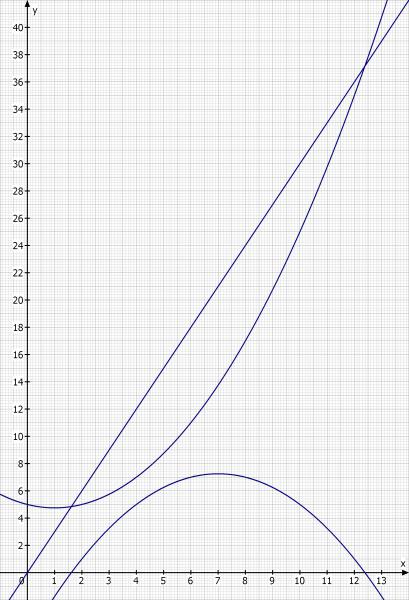
Fixkosten: K(0) = 5 GE
b) Bestimmen Sie aus der graphischen Darstellung den Bereich der Produktionsmenge, in dem der Erlös größer als die Kosten ist. Dieser Bereich heißt Gewinnzone.
Die Produktionsmenge liegt ungefähr im Bereich 1.6 < x < 12.4
c) Die Gewinnzone kann auch mithilfe der Gewinnfunktion G ermittelt werden, wobei G(x) = E(x) - K(x) gilt. Bestimmen sie einen Term von G und berechnen sie deren Nullstellen. Vergleichen sie mit dem Ergebnis aus Teilaufgabe b).
G(x) = (3·x) - (1/4·x^2 - 1/2·x + 5) = - 1/4·x^2 + 7/2·x - 5 = 0
x = 7 ± √29
x = 1.614835192 ∨ x = 12.38516480