Hallo :-)
Im Prinzip musst du das zweite Glasstück ,,passend" hinschieben. Ok, Drehen wäre vielleicht auch möglich, aber das würde sehr sehr eklig vom Rechnen werden. Du suchst also Parameter \(a,b,c\in \mathbb{R}\), sodass du für \(a\cdot f(x+b)+c\) dieselbe Flächengröße bekommst, sich auf der rechteckigen Glasplatte befindet, aber beide Flächengrenzen sich bestenfalls nur berühren. Nun soll aber die Grundform nicht verbogen werden, sodass schonmal \(a\in \{-1,1\}\) gilt:
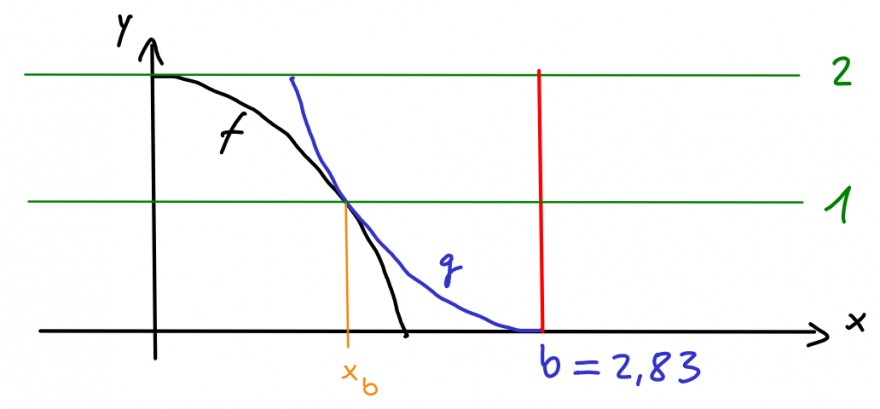
Für \(a=1\) wird das schonmal nicht klappen, da das Rechteck nur \(2.83\) m breit ist.
\(f(x_b)=1\), also \(-\frac{1}{2}\cdot x_b^2+2=1\quad \Rightarrow x_b=\sqrt{2}\approx 1.4142\).
Also ist \(x_b\) fast mittig. Jetzt kannst du \(g\) so wählen, sodass \(x_b\) gemeinsamer Berührpunkt mit \(f\) ist. Dann hast du also eine Verschiebung von \(2\cdot \sqrt{2}\approx 2.8284<2.83\) für \(g\). Da das Brett sogar \(2.83m\) breit ist, empfiehlt es sich eine Verschiebung von \(2.83\) für \(g\) zu wählen, weil es einfacher mit dem Rechnen wird. Außerdem schneiden sich so beide Funktionen in keinem Punkt.
Insgesamt hat man \(g(x)=-f(x-b)=\frac{1}{2}\cdot (x-2.83)^2\).
Jetzt kann man noch die folgenden Integrale berechnen:
\(\int_0^2 f(x)\ dx=...=\frac{8}{3}\) und
\(\int_{\underbrace{2.83-2}_{=0.83}}^{2.83} (2-f(x-2.83))\ dx=...=\frac{8}{3}\)