Aufgabe:
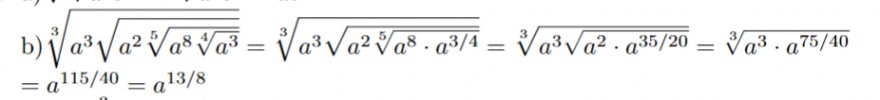
Text erkannt:
b) \( \sqrt[3]{a^{3} \sqrt{a^{2} \sqrt[5]{a^{8} \sqrt[4]{a^{3}}}}}=\sqrt[3]{a^{3} \sqrt{a^{2} \sqrt[5]{a^{8} \cdot a^{3 / 4}}}}=\sqrt[3]{a^{3} \sqrt{a^{2} \cdot a^{35 / 20}}}=\sqrt[3]{a^{3} \cdot a^{75 / 40}} \)
\( =a^{115 / 40}=a^{13 / 8} \)
Problem/Ansatz:
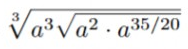
Text erkannt:
\( \sqrt[3]{a^{3} \sqrt{a^{2} \cdot a^{35 / 20}}} \)
wie kommt man auf a^35/20
Text erkannt:
b) \( \sqrt[3]{a^{3} \sqrt{a^{2} \sqrt[5]{a^{8} \sqrt[4]{a^{3}}}}}=\sqrt[3]{a^{3} \sqrt{a^{2} \sqrt[5]{a^{8} \cdot a^{3 / 4}}}}=\sqrt[3]{a^{3} \sqrt{a^{2} \cdot a^{35 / 20}}}=\sqrt[3]{a^{3} \cdot a^{75 / 40}} \)
\( =a^{115 / 40}=a^{13 / 8} \)