Flächeninhalt von einer Ganzrationalen Funktion und Gerade?

Question

Aufgabe:

Flächeninhalt von einer Ganzrationalen Funktion und Gerade?

Problem/Ansatz:

Aufgabe: Die y-Achse, die Gerade und der Graph K begrenzen, für ≤ 0, zwei Flächen. Beweisen Sie, dass diese Flächen denselben Flächeninhalt haben.

Wie berechnet man den Flächeninhalt? was bedeutet begrenzen? und wie für für ≤ 0 zwei Flächen?

Answer 1

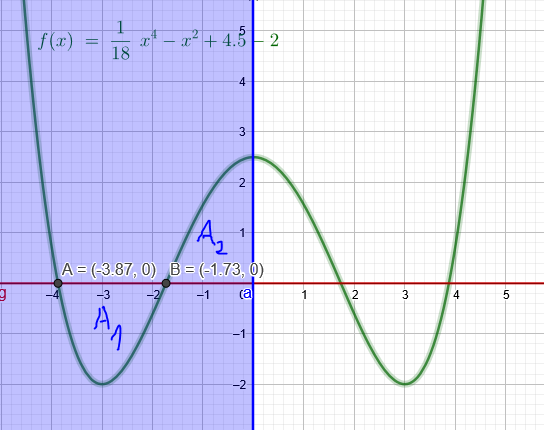
Ich kann mir denken, dass es sich um f(x)=1/18x^4-x^2+4,5 handelt. Die beiden Schnittpunkte mit g(x)=2 hast ja schon. x₁= -\( \sqrt{15} \)     x₂=-\( \sqrt{3} \)

Zur besseren Vorstellung verschiebe ich beide Funktionen um 2 Einheiten nach unten ( siehe Zeichnung)

p(x)=1/18x^4-x^2+4,5-2=1/18x^4-x^2+2,5 und h(x)=0

Text erkannt:

\( A_{1}=\int \limits_{-\sqrt{15}}^{-\sqrt{3}}\left(\frac{1}{18} x^{4}-x^{2}+2,5\right) \cdot d x=\ldots \)
Falls die Fläche negativ ist, mach Betragsstriche beidseitig \( z \cdot b \cdot:|-4|=4 \)
\( A_{2}=\int \limits_{-\sqrt{3}}^{0}\left(\frac{1}{18} x^{4}-x^{2}+2,5\right) \cdot d x=\ldots \)
Nun vergleiche die beiden Flächen.

Comments

Ich habe mehrere Methoden versucht und probiert, komme aber entweder nur auf 0 oder verschiedene antworten. Wie rechnet man den Flächeninhalt aus? :(

Answer 2

Hallo

die Gerade schneidet deine Funktion, wenn du das skizzierst offensichtlich so dass zwischen Gerade und Funktion (und y-Achse 2 Gebiete liegen. ohne Skizze oder Kenntnis der Fkt. kann man das nicht genauer sagen, aber du kannst ja plotlux nutzen um die 2 Funktionen zu platten, dann musst du die 2 Flachen mit den durch Schnittpunkte gegebenen Grenzen  die Differenz f-g integrieren.

einfachstes Beispiel f(x)=x^3, g(x)=x

 ~plot~ x^3;x ~plot~

Gruß lul

Answer 3

Wie berechnet man den Flächeninhalt?

Mit Integralen. In deinem Fall ist der Integrand die Differenz aus den Funktionstermen von ganzrationaler Funktion und Gerade.

was bedeutet begrenzen?

Es gibt eine geomtrische Figur, deren Rand aus einem Teil der y-Achse, einem Teil der Geraden und einem Teil des Graphen K besteht. Man kann um diese Figur einen Kreis zeichnen.

und wie für für ≤ 0 zwei Flächen?

Das ist unverständlich.