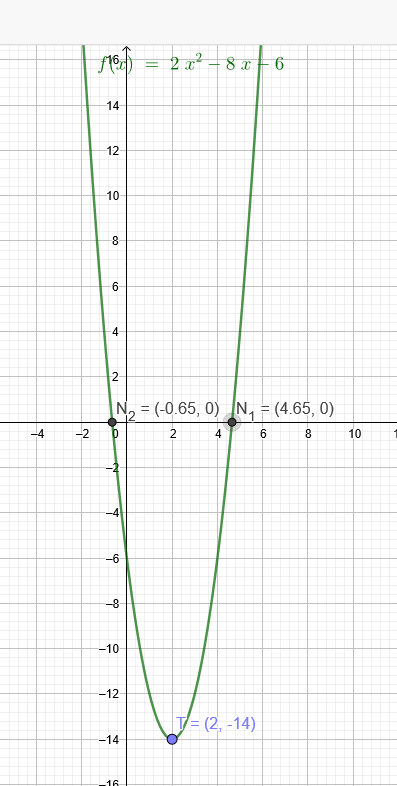
Gegeben ist die Funktion f(x) = 2x^2 -8x -6
a) Berechnen Sie die Nullstellen
2x^2 - 8x - 6=0
x^2-4x=3
(x-2)^2=3+4=7|\( \sqrt{} \)
1.) x-2 =\( \sqrt{7} \)
x₁=2+\( \sqrt{7} \)≈4,65
2.) x-2 =-\( \sqrt{7} \)
x₂ = 2 - \( \sqrt{7} \)≈-0,65
y- Achsenabschnitt der Funktion.
f(0) = - 6
b) Weisen Sie nach, dass die Extremstelle bei x = 2 liegt. Liegt dort ein Hoch- oder ein Tiefpunkt.
f´(x) = 4x -8
4x -8=0
x=2
f´´(x) = 4 > 0 also Tiefpunkt