Aufgabe: Ballonfahrt
Ein Heißluftballon war bei einer
Ballonfahrt einen Zeitraum von 48
Minuten in der Luft. Zur Vereinfachung
gelte die Annahme, dass er sich nur in
zwei Richtungen fortbewegt hat: In
Richtung Norden und bei Drehung des
Windes in Richtung Süden. An Bord des
Ballons befand sich ein Messgerät für die
Geschwindigkeit, die der Ballon in
Richtung Norden fuhr. Diese
Geschwindigkeit wurde in Abhängigkeit von der vergangenen Zeit in ein Koordinatensystem eingetragen. Vom Start bis zur Landung des Ballons ergab sich dabei das abgebildete Schaubild.
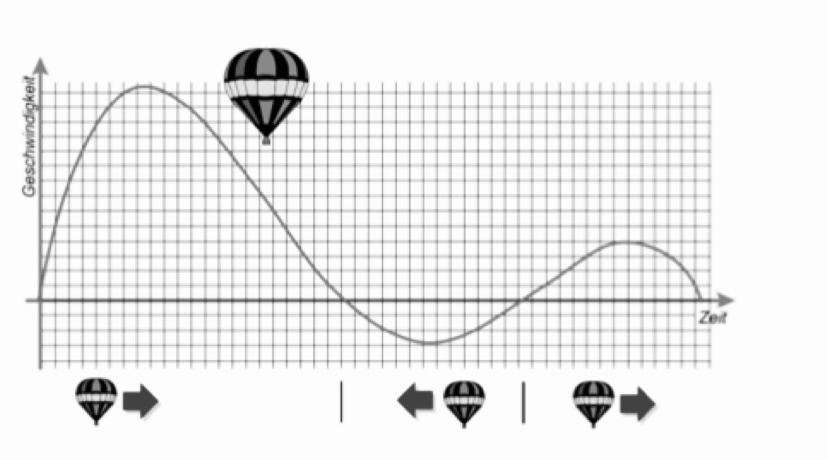
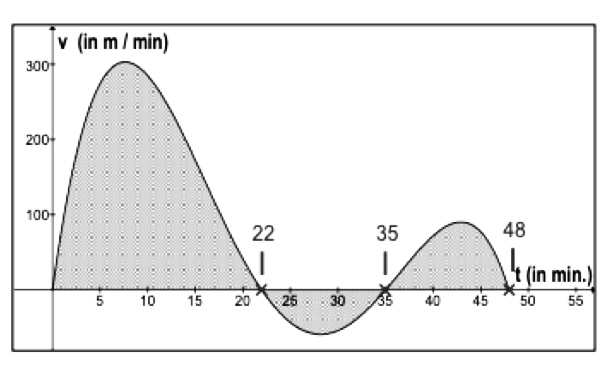
a. Beschreiben Sie den Verlauf des Graphen im Sachzusammenhang und gehen Sie hierbei auf die Bedeutung von negativen Funktionswerten, Nullstellen, Extremstellen und Flächen, die der Funktionsgraph mit der x-Achse einschließt, ein.
b. Die Ballonfahrt lässt sich in Bezug auf Geschwin- digkeit und Zeit näherungsweise durch folgende Funktionsgleichung modellieren:
() = −0,00254 + 0,26253 − 8,7652 + 92,4 mit 0 ≤ ≤ 48, : Zeit in Minuten,
(): Geschwindigkeit in Richtung Norden in m/min
Bestimmen Sie das Integral ∫22 0 () und interpretieren Sie diesen Wert. Wiederholen Sie dies für das
Integral ∫35 22 ().
c. Ermitteln Sie die Strecke, die der Ballon bis zur Landung in der Luft insgesamt zurückgelegt hat (unabhängig von der Richtung, in die er geflogen ist)
d. Berechnen Sie ∫48 0 () und vergleichen Sie diesen Wert mit Ihren Ergebnissen aus den
Aufgabenteilen b) und c). Welche Bedeutung hat dieser Wert im Sachzusammenhang?
e. Formulieren Sie in einem kurzen Text Erkenntnisse in Bezug auf den Zusammenhang zwischen Integral und Inhalte von Flächen zwischen Funktionsgraph und x-Achse.
f. Formulieren Sie einen Ansatz, wie man berechnen könnte, wann sich der Ballon 4 km nördlich vom Startpunkt befindet. Begründen Sie auch, warum es hier mehrere Ergebnisse geben kann.
Zusatz: Bestimmen Sie die Ergebnisse näherungsweise oder mit Hilfe von geeigneter Software exakt.
Frage/Problem:
- verstehe nicht wie ich die Aufgaben lösen soll. Vielleicht kann mir jemand helfen