Textaufgabe( Integrale, Polynomfunktion, Gleichung aufstellen)

Question

Aufgabe: Eine Polynomfunktion 4. Grads hat im Ursprung einen Wendepunkt mit waagrechter Tangente und schneidet die x - Achse an der Stelle x = 5.

Der Flächeninhalt , den der Funktionsgraph mit der X - Achse einschließt , beträgt 31,25 E. Ermittle die beiden möglichen Funktionsgleichungen der Polynomfunktion .

Problem/Ansatz: Hallo, ich bin beim lernen auf diese Aufgabe gestoßen und weiß nicht weiter. Könnte mir jemand helfen?

Answer 1

Eine Polynomfunktion 4. Grads hat im Ursprung einen Wendepunkt mit waagrechter Tangente.

Daher der Ansatz

f(x)=ax⁴ +bx³

Nullstellen (Integrationsgrenzen) x=0 und x=-b/a

...schneidet die x - Achse an der Stelle x = 5

(1) 0=625a+125b

Der Flächeninhalt , den der Funktionsgraph mit der X - Achse einschließt , beträgt 31,25

|\( \int\limits_{0}^{-b/2} \) (ax⁴ +bx³) dx|=31,25 führt zu

(2) |\( \frac{b^5}{20a^4} \)|=31,25

Löse das System (1); (2).

Comments

Vielen vielen Dank!!!

Answer 2

Die Funktion lautet:

f: y = ax⁴ + bx³ + cx² + dx + e

f ': y = 4ax³ + 3bx² + 2cx + d

f '': y = 12ax² + 6bx + 2c

F: y = 1/5ax⁵ + 1/4bx⁴ + 1/3cx³ + 1/2dx² + ex (+ const.)

Die Informationen im Text ergeben, in der Reihenfolge ihres Auftretens, folgendes Gleichungssystem:

f (0) = 0

f '' (0) = 0

f ' (0) = 0

f (5) = 0

F (5) - F (0) = ± 31.25

Dieses System hat die Lösungen:

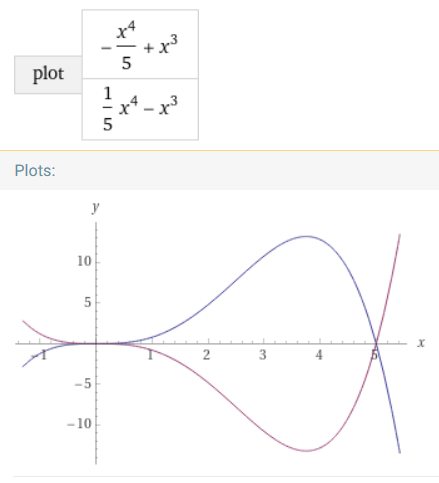
a = ∓ 1/5, b = ± 1, c = d = e = 0

D.h. die beiden Funktionen sind: