Hallo,
Ich weiß nicht wie man das rechnet?
am besten gar nicht! Sondern man muss es verstehen; dann ist es auch wirklich einfach ;-)
mache Dir klar, was die Parameterform einer Gerade besagt. Dazu folgendes Bild.
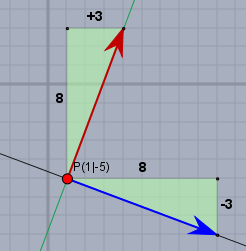
Dort siehst Du den Punkt \(P(1|\,-5)\) und den blauen Richtungsvektor \(\vec r(8|\,-3)\). Die schwarze Gerade \(g\) $$g: \quad \vec x = P + t \cdot \vec r = \begin{pmatrix}5\\ -1\end{pmatrix} + t\cdot \begin{pmatrix}8\\ -3\end{pmatrix}$$ist mit diesen beiden Größen in der Parameterform gegeben. Jeder Punkt auf der Geraden lässt sich über einen Wert für \(t\) erreichen.
Möchtest Du die Richtung der Geraden ändern, so musst Du die Koordinaten von \(\vec r\) ändern. Und wenn die neue Gerade senkrecht auf der alten stehen soll, so muss das 'Koordinatendreieck' um eine viertel Umdrehung 'umgeklappt' werden. Das erreicht man dadurch, indem man die beiden Koordinaten vertauscht und eine von beiden negiert.
Schau Dir das auf dem Bild an, dann sollte das klar sein. Eine Gerade \(s\) (grün), die senkrecht auf \(g\) steht, kann also lauten$$s: \quad \vec x = \begin{pmatrix}5\\ -1\end{pmatrix} + t\cdot \begin{pmatrix}3\\ 8\end{pmatrix}$$Gruß Werner