Gesamtkosten-funktion 3 Grades
K(x) = ax3 + bx2 + cx + d
Die Fixkosten betragen 12,5 GE
a*03 + b*02 + c*0 + d = 12,5
Wenn 1 ME produziert wird,betragen die Gesamtkosten 16,75 GE
a*13 + b*12 + c*1 + d = 16,75
wenn 2 ME produziert werden,betragen sie 18,5 GE
a*23 + b*22 + c*2 + d = 18,5
Die Maximalen Gesamtkosten betragen 42,25 GE
d/dx K(x) = 3ax2 + 2bx + c = 0
ax3 + bx2 + cx + d = 42,25
Dieses Gleichungssystem mit 5 Gleichungen in 5 Unbekannten hat zwei Lösungen, nämlich
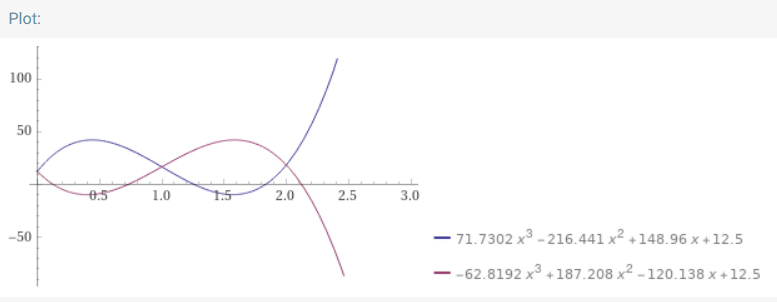
und nur die rote Linie entspricht dem geforderten Kostenmaximum im Intervall von 0 bis 7. Die Gesamtkosten sinken also, je mehr man produziert. Wer hat sowas erfunden?