Hallo,
ich korrigiere mal einen Satz in Deiner Frage, so wie ich ihn verstanden habe:
Sei \(x \neq 0 \) ein Punkt in \( \mathbb{R}^{2}\). Dieser definiert eine Gerade \(G(0, x)= \{t x_1 |\, t x_2 \}\) mit \(t \in \mathbb{R} \)
Die Skizze sollte IMHO etwa so aussehen
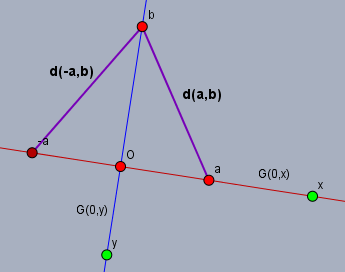
Wenn \(d(a,b) = d(-a,b)\) (die lila Strecke gleich lang sind) stehen \(G(0,x)\) und \(G(0,y)\) senkrecht zu einander.
Und wenn man nun davon ausgeht, dass für die Punkte \(a\) und \(b\) gilt$$a= (\alpha x_1|\, \alpha x_2) \quad \alpha \in \mathbb R \\b = (\beta y_1|\, \beta y_2) \quad \beta\in \mathbb R $$dann berechnet sich \(d(a,b)\) lt. Definition aus$$\begin{aligned} d(a,b) &= \sqrt{\left(\alpha x_1 - \beta y_1\right)^2 + \left(\alpha x_2-\beta y_2\right)^2} \\ &= \sqrt{\left(\alpha x_1\right)^2 - 2\alpha \beta x_1y_1 + \left(\beta y_1\right)^2 + \left(\alpha x_2\right)^2- 2\alpha\beta x_2y_2+ \left(\beta y_2\right)^2} \\ &= \sqrt{\left(\alpha x_1\right)^2 + \left(\beta y_1\right)^2 + \left(\alpha x_2\right)^2 + \left(\beta y_2\right)^2- 2\alpha \beta (x_1y_1 + x_2y_2)} \\ \end{aligned}$$und der Abstand \(d(-a,b)\) zum Punkt \(-a=(-\alpha x_1|\, -\alpha x_2)\) ist dann entsprechend $$d(-a,b) = \sqrt{\left(\alpha x_1\right)^2 + \left(\beta y_1\right)^2 + \left(\alpha x_2\right)^2 + \left(\beta y_2\right)^2 + 2\alpha \beta (x_1y_1 + x_2y_2)}$$\(d(-a,b)\) unterscheidet sich von \(d(a,b)\) nur durch das Vorzeichen des letzten Summanden unter der Wurzel. Ist dieser Summand \(=0\), dann sind beide Abstände gleich. Da man lt. Vorgabe davon ausgehen kann, dass \(\alpha\) und \(\beta \ne 0\) sind, folgt daraus$$d(a,b) = d(-a,b) \Longleftrightarrow x_1y_1+x_2y_2 = 0$$Gruß Werner