Ich brauche zu den beiden Aufgaben bitte Hilfe! Ich stehe da irgendwie auf dem Schlauch..
1)

Text erkannt:
Sei \( V \) ein endlichdimensionaler Vektorraum mit Skalarprodukt \( \langle\cdot, \cdot\rangle \) und \( u \in V \) mit \( \|u\|=1 \). Zeigen Sie, dass \( f: V \rightarrow V, v \mapsto\langle v, u\rangle u \), eine Orthogonalprojektion ist (siehe \( 1 . \) Aufgabe), und bestimmen Sie Kern \( (f) \) und Bild \( (f) \).
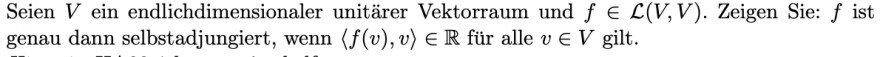
Text erkannt:
Seien \( V \) ein endlichdimensionaler unitärer Vektorraum und \( f \in \mathcal{L}(V, V) . \) Zeigen Sie: \( f \) ist genau dann selbstadjungiert, wenn \( \langle f(v), v\rangle \in \mathbb{R} \) für alle \( v \in V \) gilt.
2)