... dann ist der Radius \(r\) des kleinsten Kreises$$r = \frac R4\left( 1 - \left( \frac eR\right)^2\right)$$
... das ist natürlich nicht ohne weiteres offensichtlich ;-) Dazu zwei Bilder, \(R\) ist der Radius des großen blauen Kreises:
1.) alle Mittelpunkte der Kreise (rot), die sowohl den oberen Kreis (orange) als auch die horizontale Gerade (blau) berühren, liegen auf einer Parabel (lila), deren Brennpunkt \(B\) ist und deren Leitlinie durch \(B'\) verläuft. Der Abstand von \(K\) zur Leitline \(b\) (lila gestrichelt) muss genauso groß sein wie der Abstand von \(K\) zu \(B\). Mit \(|BE|=|EB'|\).
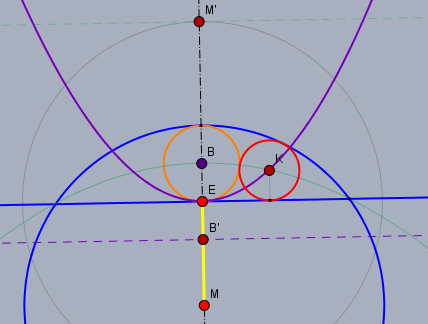
Sei der horizontale Abstand von \(K\) zur Senkrechten durch \(M\) gleich \(x\), so gilt hier$$2(R-e)r = x^2, \quad e =|EM|$$
2.) Die Mittelpunkte aller Kreise (rot), die sowohl den blauen Kreis als auch die Horizontale (blau) berühren liegen auf der grünen Parabel mit Brennpunkt \(M\) und Leitlinie \(m\) (grün gestrichelt) durch \(M'\). Der Abstand von \(K\) zu \(m\) ist genauso groß wie der von \(K\) zu \(M\). Hier ist \(|M'B|=|BM|\).
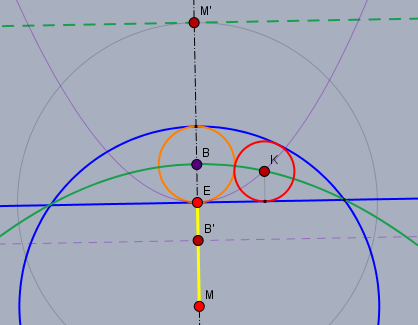
mit \(|BE|=(R-e)/2\) gilt für diese Parabel$$2(R+e)\left(\frac{R-e}2-r\right) = x^2$$Gleichsetzen dieser Parabelgleichungen gibt dann$$\begin{aligned}2(R-e)r&=2(R+e)\left(\frac{R-e}2-r\right)\\2Rr - 2er&= R^2-e^2 -2Rr-2er&&|\,+2Rr+2er\\4Rr &= R^2-e^2&&|\,\div 4R\\ r&= \frac R4\left(1-\left(\frac eR\right)^2\right)\end{aligned}$$