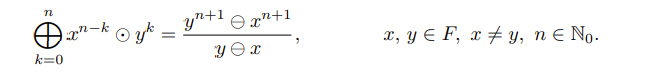
Text erkannt:
\( \bigoplus_{k=0}^{n} x^{n-k} \odot y^{k}=\frac{y^{n+1} \ominus x^{n+1}}{y \ominus x}, \quad x, y \in F, x \neq y, n \in \mathbb{N}_{0} \)
Diese Formel soll ich durch vollständige Induktion beweisen. Den Induktionsanfang habe ich bereits mit n= 0 gezeigt. Der Induktionsschritt n+1 bereitet mir aber Probleme.
Problem/Ansatz:
Ich will die linke Seite x^(n+1-k)*y^k nach y^(n+1+1)-x^(n+1+1)/y - x umformen.
Stehe aber gerade dem Schlauch.