Hallo,
ich habe Dir das Dach mal im Geoknecht3D eingegeben. Es ist an einer Seite aufgeschnitten zur besseren Einsicht.
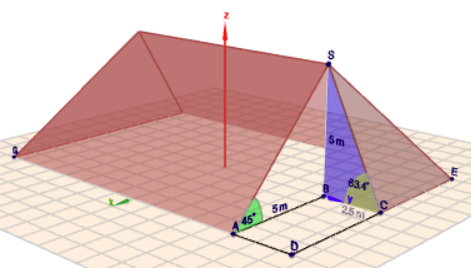
(klick auf das Bild)
Dort siehst Du das blaue rechtwinklige Dreieck mit dem gelben Winkel \(\alpha\). Und dort gilt$$\tan \alpha = \frac{5\,\text m}{2,5\, \text m}$$Den grünen Winkel \(\beta\) kannst Du ohne Taschenrechner bestimmen. Das Dreieck \(\triangle ABS\) ist gleichschenklig und rechtwinklig.
Zur Berechnung der Dachfläche berechne die Höhe \(CS\) des Dreiecks \(\triangle DES\) mit dem Pythagoras aus dem blauen Dreieck. Die Grundseite \(|DE|=10\,\text m\) ist gegeben. Dann bleiben noch die beiden trapezförmigen Dachflächen über. Die Höhe der Trapeze ist die Strecke \(AS\), die gleichzeitig Hypotenuse des Dreiecks \(\triangle ABS\) ist.
Zur Kontrolle: die Flächen für das Dreieck \(F_d\) und für das Trapez \(F_t\) sind$$F_d \approx 27,95\,\text m^2, \quad F_t\approx 88,39\,\text m^2$$
Falls Du noch Fragen hast, so melde Dich bitte.