Vom Duplikat:
Titel: Problem/Ansatz: Bestimme alle lokalen Extrema von der Funktion f !
Stichworte: extrema
Aufgabe: Mathe: Bestimme alle lokalen Extrema von f ! Die Matrix A sei eine symmetrische und positiv definite Matrix und die Matrix b sei Element des R2
Problem/Ansatz: Guten Tag ich verstehe nicht ganz genau wie ich mit dem Gradienten und der Hesse Matrix die lokalen Extrema bestimmen kann, denn wenn ich den Gradienten bestimme bekomme ich eine Matrix mit vielen Variablen .Weiß jemand wie man hier die lokalen Extrema berechnet ?
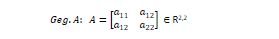
\( \vec{b} \) ∈ R2 , f : R2 → R , \( \vec{x} \) → ⟨\( \vec{x} \), 1/2 A\( \vec{x} \) + \( \vec{b} \)⟩