Diskussion rationaler Funktionen

Question

Gegeben ist folgendes Problem:

In welchen Punkt des Funktionsgrafen f(x) = xhoch5 - 3xhoch2 + 2x -4 verläuft die Tangente an den Graphen parallel zu der Geraden y = 2x + 9.

Ich habe es auf dieser Weise probiert, dennoch ohne Erfolg die Lösungen wären:

p1 = (0 |-4) p2 (1,063 | -3,91)

bitte um ausführliche erklärung.

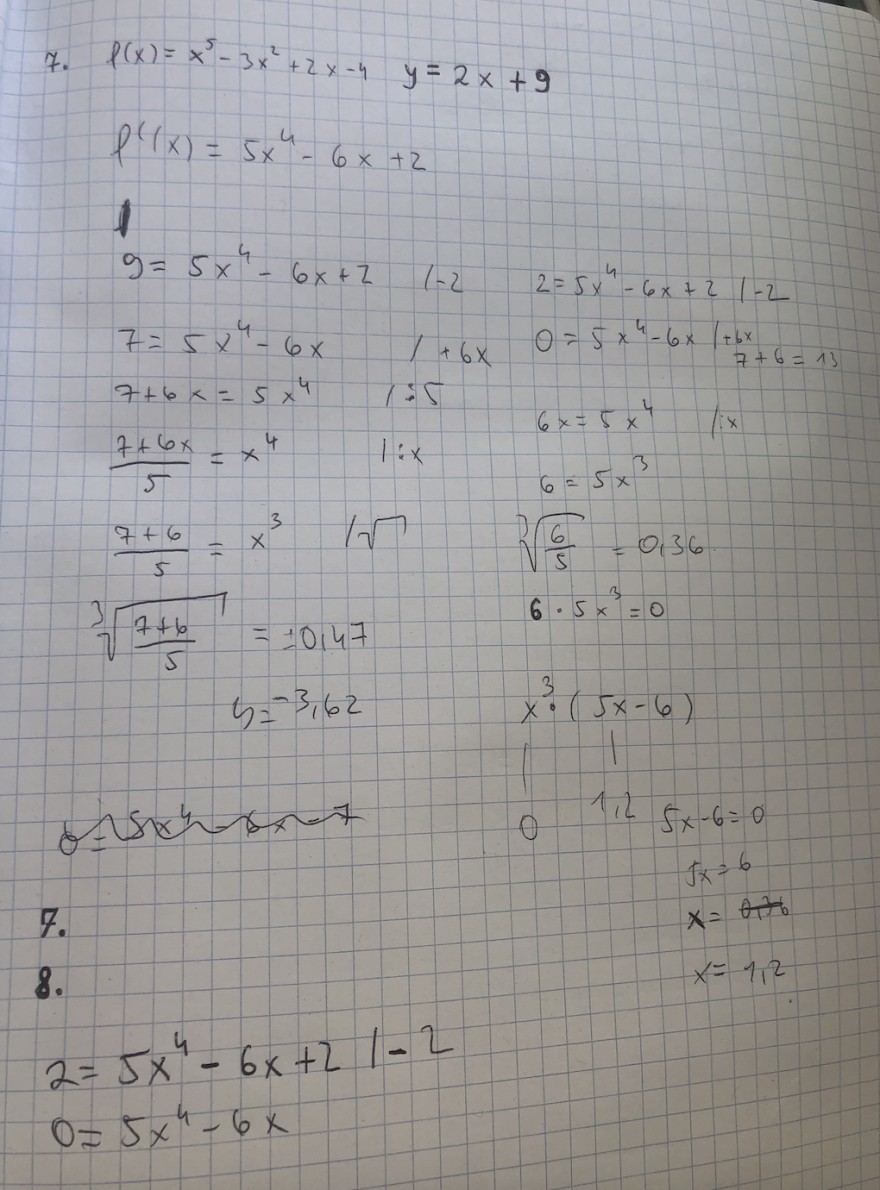
Text erkannt:

\( 7 . \)
\( x=\theta+6 \)
\( 8 . \)
\( =1,2 \)
\( 2=5 x^{4}-6 x+21-2 \)
\( 0=5 x^{4}-6 x \)

Answer 1

Wo haben f(x) und die Tangente an f(x) die gleiche Steigung, wie die gegebene Gerade (nämlich 2)?

D.h. für welches x gilt 5x⁴-6x+2=2? Nach Subtraktion von 2 auf beiden Seiten:

5x⁴-6x=0 oder x(5x³-6)=0

Ein Produkt ist 0, wenn ein Faktor 0 ist:

x₁=0 oder 5x₂³-6=0 bzw. x₂=\( \sqrt[3]{1,2} \).

Beide Lösungen in f(x)=x⁵ - 3x² + 2x -4 eingesetzt, ergibt die y-Werte der gesuchten Punkte.

Comments

!

Answer 2

f(x)=x^5-3x^2+2x-4          y=2x+9

f´(x)=5x^4-6x+2                y´=2

5x^4-6x+2 =2

5x^4-6x=0

x*(5x^3-6)=0

x₁=0      f(0)=-4 

5x^3-6=0

x^3=\( \frac{6}{5} \)=1,2

x₂=\( \sqrt[3]{1,2} \)≈1,06     f(1,06)=1,06^5-3*1,06^2+2*1,06-4≈-3,9

Comments

!