Text erkannt:
\( T(0)=3 \)
\( T(n)=(T(n-1))^{2} \)
\( T(1)=9 \)
\( T(2)=81 L 9 \)
\( T(3)=6561^{2} \)
\( a_{h}= \)
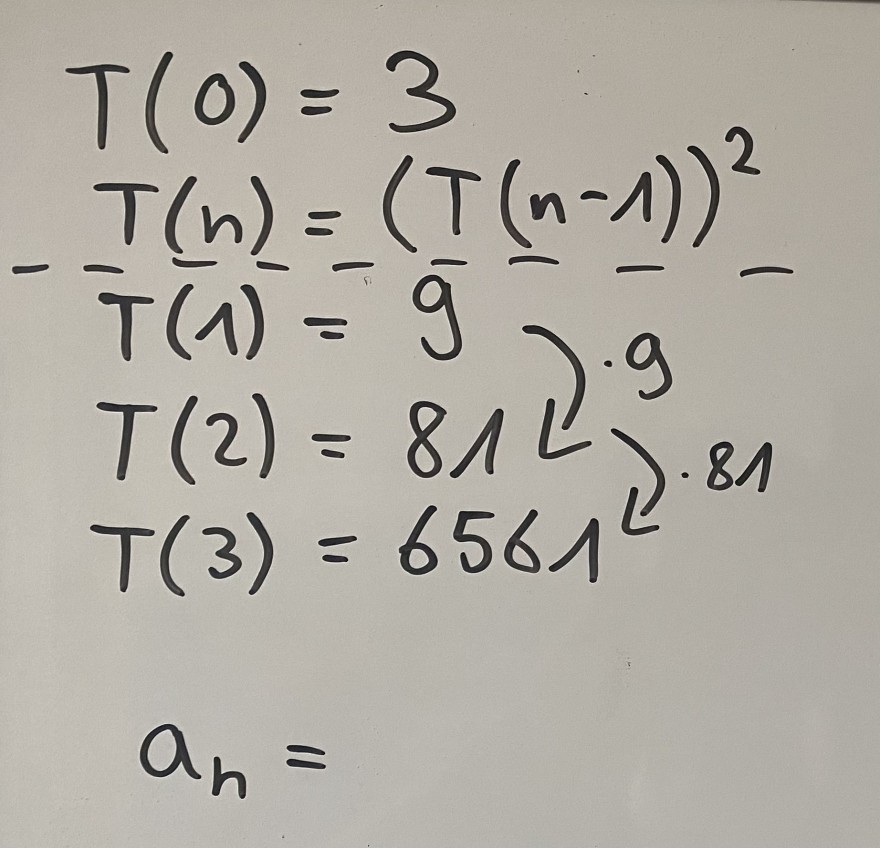
Text erkannt:
\( T(0)=3 \)
\( T(n)=(T(n-1))^{2} \)
\( T(1)=9 \)
\( T(2)=81 L 9 \)
\( T(3)=6561^{L} .81 \)
\( a_{h}= \)
Wie nennt man diese Art von Folgen wenn man immer mit dem vorherigen Folgeglied multipliziert? Kann mir jemand da helfen die explizite Form aufzustellen indem er oder sie mir Tipps gibt?