Wie groß ist die wirksame Hebekraft Fh auf der Hand in 6 cm Entfernung vom Drehpunkt?

Question

Aufgabe:

Die Skizze veranschaulicht die Kräfteverhältnisse, wie sie etwa
beim Heben einer Last mit der Hand auftreten. Die Zugkraft am
Muskel, der am Unterarm unter einem Winkel von 40° angreift,
beträgt 1500 N.
Wie groß ist die wirksame Hebekraft Fh auf der Hand in 6 cm
Entfernung vom Drehpunkt? Kann damit eine Masse von 10 kg
gehoben werden ?

Problem/Ansatz:

hallo,

auch hier bräuchte ich eure Hilfe.

Answer 1

Hallo,

wenn man sich die entscheidenden Größen heraus zeichnet ...

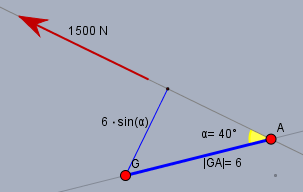
... dann bleibt als Hebel \(6\,\text{cm} \cdot \sin(\alpha)\) und das Moment \(M\) ist $$M = 6\,\text{cm} \cdot \sin(\alpha) \cdot F_z =  6\,\text{cm} \cdot \sin(40°) \cdot1500\,\text N \approx 57,85\,\text{Nm}$$und damit wird \(F_h\) zu$$M = 36\,\text{cm} \cdot F_h \implies F_h = \frac{M}{0,36\,\text{m}} = \frac{57,85\,\text{Nm}}{0,36\,\text{m}} \approx 160,7\,\text N$$und das ist mehr als die ca. 98,1N, mit der eine Masse von 10kg angehoben werden müsste.