Danke nur weiß ich jetzt leider nicht wie ich dieses Ergebnis im Sachzusammenhang interpretieren kann
Die Aufgabe lautet doch, einen Punkt \(P\) zu finden, der sich auf der X-Achse befindet, und folglich die Koordinaten \(P(x|\,0)\) hat. Die Bedingung ist, dass dieser Punkt einen möglichst kleinen Abstand \(d\) zu einem zweiten Punkt \(A(3|\,1)\) hat.
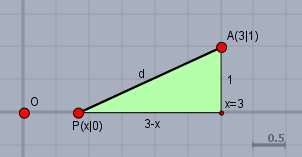
Der Abstand \(d\) (schwarz) ist von \(x\) abhängig und berechnet sich nach Pythagoras$$d^2 = (3-x)^2 + 1^2$$also ist die Funktion \(d(x)\)$$d(x) = \sqrt{(3-x)^2 + 1} \to \min$$und für diese Funktion soll das Minimum gefunden werden, d.h. die Position \(x\) bei der \(d\) am kleinsten.
Offensichtlich ist dies bei \(x=3\) der Fall, wenn \(P\) direkt unterhalb von \(A\) positioniert wird.