zweimal stetig differenzierbare Funktion

Question

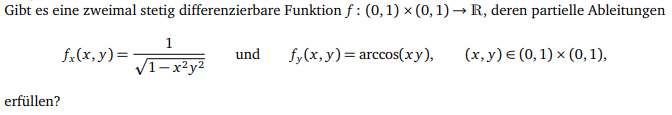
Text erkannt:

Gibt es eine zweimal stetig differenzierbare Funktion \( f:(0,1) \times(0,1) \rightarrow \mathbb{R} \), deren partielle Ableitungen
$$ f_{x}(x, y)=\frac{1}{\sqrt{1-x^{2} y^{2}}} \quad \text { und } \quad f_{y}(x, y)=\arccos (x y), \quad(x, y) \in(0,1) \times(0,1) $$
erfüllen?

Könnte mir hier jemand helfen?

Answer 1

Aloha :)

Für eine solche Funktion \(f(x;y)\) müsste gelten:$$f_{yx}(x;y)=f_{xy}(x;y)$$Wir prüfen das nach, indem wir die Ableitungen bilden und vergleichen:$$f_{yx}(x;y)=\frac{\partial f_x}{\partial y}=\frac{\partial}{\partial y}\frac{1}{\sqrt{1-x^2y^2}}=\frac{x^2y}{(1-x^2y^2)^{3/2}}$$$$f_{xy}(x;y)=\frac{\partial f_y}{\partial x}=\frac{\partial}{\partial x}\arccos(xy)=-\frac{y}{(1-x^2y^2)^{1/2}}$$

Hmmm, die beiden Ableitungen sind ungleich, also gibt es keine solche Funktion \(f(x;y)\).