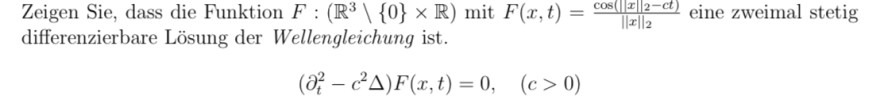
Huhu, Ich habe Probleme bei der folgenden Aufgabe.
Meine Idee wäre, erstmal mit der zweiten partiellen Ableitung von F zu starten (nach t) und dann den Laplace-Operator zu berechnen. Als letztes würde ich vermuten, dass ich die Wellengleichung noch überprüfen muss, dabei habe ich allerdings große Schwierigkeiten. Ich wäre euch daher vor allem über Hilfe bei Schritt 3 dankbar, aber auch bei Schritt 2 bin ich mir noch unsicher.
Ganz davon abgesehen, weiß ich auch gar nicht, ob ich mit meiner Idee überhaupt auf dem richtigen Weg bin.
Danke euch im Voraus :)