bestimme den Tiefsten Punkt

Question

Aufgabe:

Tiefpunkt bestimmen

f '(x)=  1/4 e^(1/8 x-9/5)-1/4 e^(-1/8 x+9/5)

Problem/Ansatz:

wie kann ich dieser Funktion gleich null setzen ganz detailliert

Answer 1

Hallo

dividiere durch 1/4 e^(-1/8 x+9/5) dann die verbleibende e- funktion auf eine Seite, Zahlen auf die andere und ln anwenden. Ich hoffe, das ist ganz detailliert!

Gruß lul

Answer 2

1/4 e^(1/8 x - 9/5) - 1/4 e^(-1/8 x + 9/5) = 0

1/4 e^(1/8 x - 9/5)  = 1/4 e^(-1/8 x + 9/5)

1/8x - 9/5  = -1/8x + 9/5

Answer 3

\( f^{\prime}(x)=\frac{1}{4} e^{\frac{1}{8} x-\frac{9}{5}}-\frac{1}{4} e^{-\frac{1}{8} x+\frac{9}{5}} \)
\( \frac{1}{4} e^{\frac{1}{8} x-\frac{9}{5}}-\frac{1}{4} e^{-\frac{1}{8} x+\frac{9}{5}}=0 \mid \cdot 4 \)
\( e^{\frac{1}{8} x-\frac{9}{5}}-e^{-\frac{1}{8} x+\frac{9}{5}}=0 \)
\( e^{\frac{1}{8} x-\frac{9}{5}}=e^{-\frac{1}{8} x+\frac{9}{5}} \)
Vergleich der Expononenten:
\( \frac{1}{8} x-\frac{9}{5}=-\frac{1}{8} x+\frac{9}{5} \mid+\frac{9}{5}+\frac{1}{8} x \)
\( \frac{2}{8} x=\frac{18}{5} \mid \cdot \frac{8}{2} \)
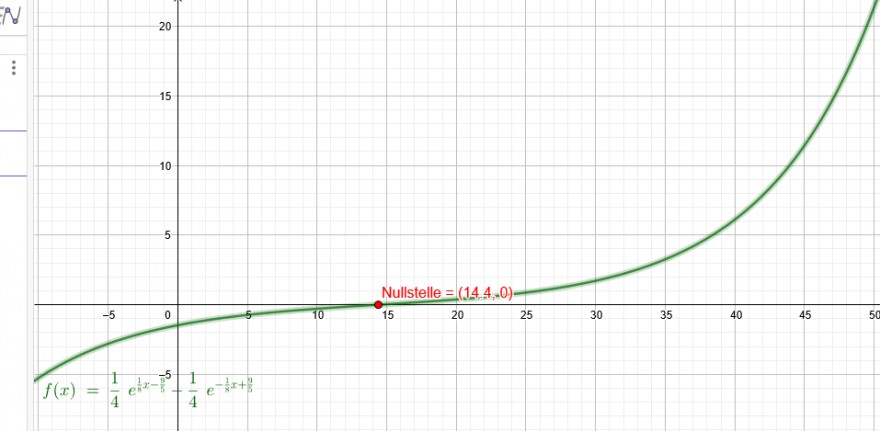
\( x=\frac{18}{5} \cdot \frac{8}{2}=14,4 \)