Ich kenne keinen anderen Weg:
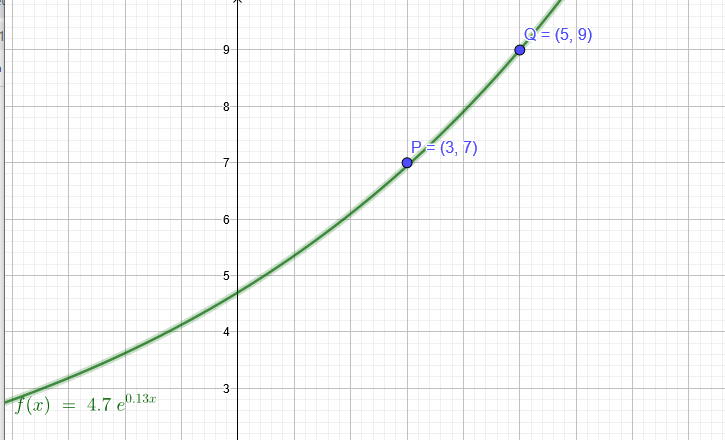
\( P(3 \mid 7) \)
1.) \( 7=a \cdot e^{3 b} \rightarrow a=\frac{7}{e^{3 b}} \)
\( Q(5 \mid 9) \)
2.) \( 9=a \cdot e^{5 b} \rightarrow a=\frac{9}{e^{5 b}} \)
\( \frac{7}{e^{3 b}}=\frac{9}{e^{5 b}} \)
\( \frac{e^{5 b}}{e^{3 b}}=\frac{9}{7} \)
\( e^{2 b}=\frac{9}{7} \)
\( 2 b=\ln \left(\frac{9}{7}\right) \)
\( b=\frac{\ln \left(\frac{9}{7}\right)}{2} \approx 0,13 \)
\( a \approx \frac{9}{e^{5 \cdot 0,13}} \approx 4,7 \)
\( y=4,7 \cdot e^{0,13 x} \)