Warum klappt das bei der oberen, aber bei der unteren nicht?

Question

4-Feldertafel:

Gegeben ist folgende 4-Feldertafel:

Text erkannt:

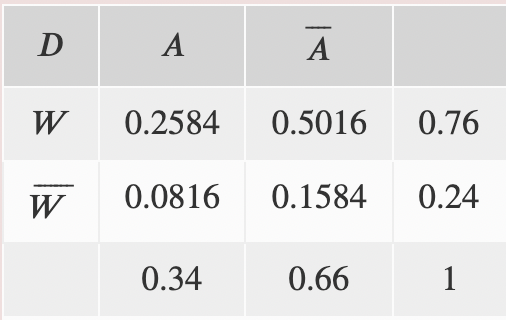
\begin{tabular}{|c|c|c|c|}
\hline\( D \) & \( A \) & \( \bar{A} \) & \\
\hline\( W \) & \( 0.2584 \) & \( 0.5016 \) & \( 0.76 \) \\
\hline \( \bar{W} \) & \( 0.0816 \) & \( 0.1584 \) & \( 0.24 \) \\
\hline & \( 0.34 \) & \( 0.66 \) & 1 \\
\hline
\end{tabular}

Die Werte innerhalb der Tafel sind Anfangs leer. Es gibt nur die am Rand...

Als Lösung wird gesagt, dass man auf die inneren Werte kommt, wenn man die äußeren multipliziert.

Bsp: 0,34*0,76=0,2584

Anschließend hab ich mich gefragt, ob das eine generelle Regel ist...

Aber in der folgenden Tafel, klappt das nicht mehr:

Text erkannt:

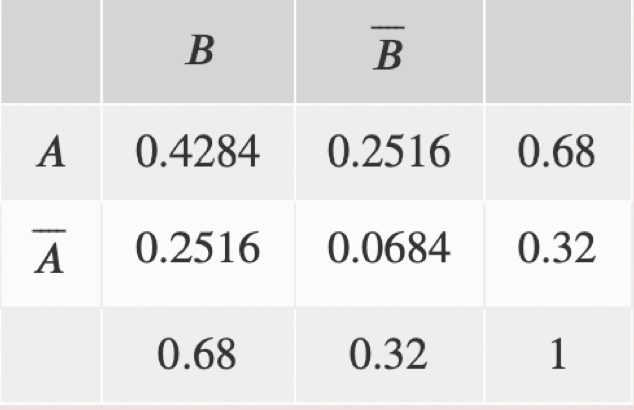
\begin{tabular}{|c|c|c|c|}
\hline & \multicolumn{1}{|c|} { B } & \( \bar{B} \) & \\
\hline\( A \) & \( 0.4284 \) & \( 0.2516 \) & \( 0.68 \) \\
\hline \( \bar{A} \) & \( 0.2516 \) & \( 0.0684 \) & \( 0.32 \) \\
\hline & \( 0.68 \) & \( 0.32 \) & 1 \\
\hline
\end{tabular}

Warum klappt das bei der oberen, aber bei der unteren nicht ?

(Die 4-Feldertafeln sind alle zu 100% richtig)

Answer 1

Das mit dem Multiplizieren gilt nur wenn die Merkmale die untersucht werden unabhängig sind.

Generell gilt das eher nicht, die Unabhängigkeit wäre ein spezialfall der eigentlich dann nicht mehr über eine Vierfeldertafel untersucht wird.

Meist nimmt man die Vierfeldertafel für abhängige Merkmale.

Comments

Wie kann man erkennen, dass es sich um unabhängige Ereignisse handelt ?

---

Für die Unabhängigkeit gilt

P(A) * P(B) = P(A ∩ B)
also wenn das mit dem multiplizieren klappt.

oder auch

P(B | A) = P(B | nA) = P(B)