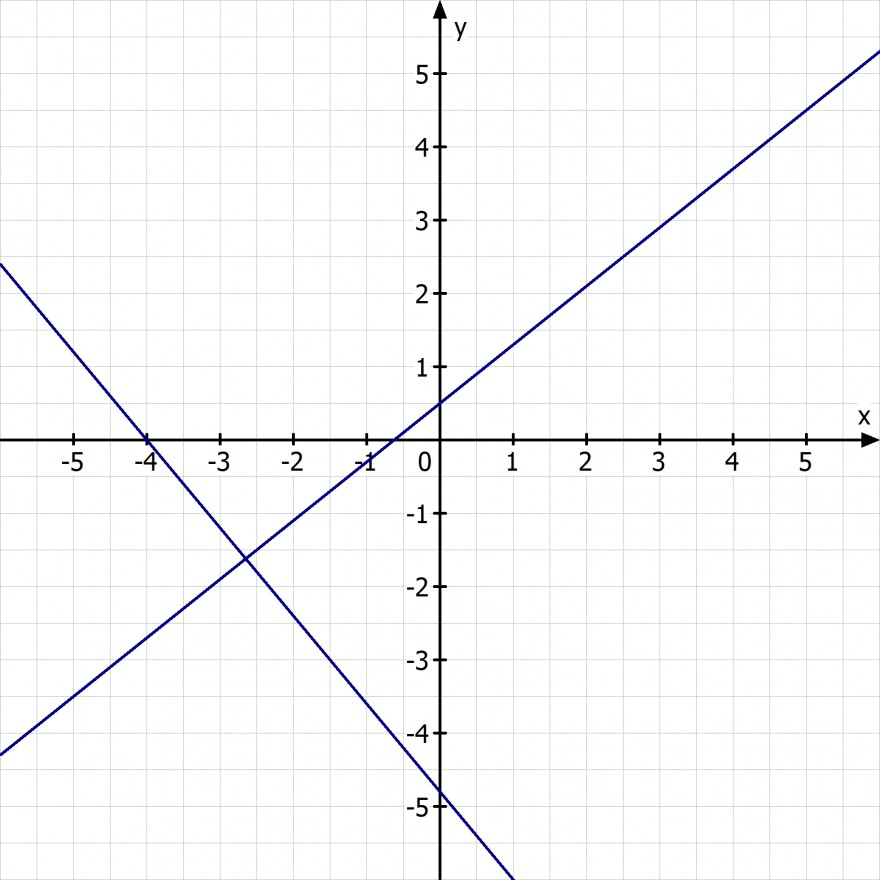
Zwei lineare Funktionen
y = mx + b und y = nx + c
stehen senkrecht aufeinander, wenn das Produkt der Steigungen -1 ergibt.
6x + 5y + 24 = 0
5y = -6x - 24
y = -6/5*x - 24/5
y = 0,8x + 0,5
y = 4/5*x + 1/2
Wir bilden das Produkt der Steigungen
-6/5 * 4/5 = -24/25 ≠ -1
Da das Produkt nicht -1 ist, stehen die Geraden nicht senkrecht zueinander. Das ist grafisch allerdings nicht immer so einfach zu sehen.