Wie groß ist die grün markierte Fläche?

Question

Aufgabe:

Die Seite a des unteren Quadrates ist 17 cm lang. Wie groß ist die grün markierte Fläche? Runde das Ergebnis auf eine Nachkommastelle.

Problem/Ansatz:

Ich glaube, dass man die Fläche des großen Dreieck minus die Fläche des kleinen Dreiecks rechnet. Aber wie soll man die Fläche des kleinen Dreieck berechnen?

Answer 1

Das kleine Dreieck ist Ähnlich zu dem Dreieck aus dem kleinen Dreieck plus der grünen Fläche.

In welchem Längenverhältnis stehen die beiden Hypotenusen zueinander und in welchem Verhältnis stehen dann die beiden Dreiecksflächen zueinander.

Zum Lösungsvergleich hier eine Skizze von geogebra

Comments

Wie kann ich die Längenverhältnisse berechnen?

---

Die eine Länge über den Pythagoras und die andere ist direkt die Hälfte von a. Das solltest du notfalls auch begründen können.

Aber Dreieck ABE und Dreieck DAG sind sicher kongruent.

---

H_D ... Hypotenusenlänge des großen Dreiecks ABF

H_d ... Hypotenusenlänge des kleinen Dreiecks AEG

A_D ... Flächeninhalt des großen Dreiecks ABF

Ad ... Flächeninhalt des kleinen Dreiecks AEG

Ag ... Größe der grünen Fläche

H_D = \( \frac{a}{2} \) • \( \sqrt{5} \) 

H_{d =} \( \frac{a}{2} \)

H_D : H_d = (\( \frac{a}{2} \) • \( \sqrt{5} \) )  : ( \( \frac{a}{2} \)) = \( \sqrt{5} \) /1

Weil die Flächeninhalte ähnlicher Dreiecke sich zueinander verhalten, wie die Quadrate ihrer Seitenlängen, folgt daraus:

A_D : A_d = 5/1

A_g = A_D - A_d = a²/4 - a²/ 20 = 0,2 a²

---

Prima gemacht. Also wenn der Fragesteller es nicht alleine hinbekommen sollte, dann wäre das eine sehr schöne Lösung.

---

Danke, aber ich habe ja nur umgesetzt, was du geschrieben hast.

"Beste Antwort" hast du gegeben, wegen deines eleganten Lösungsvorschlags und der schönen Zeichnung.

Answer 2

Also ganz klar sollte ja sein dass das große Dreieck die Fläche (a*a/2)/2, demnach a^2/4 hat.

Wenn du in der ganzen Figur die fehlenden Winkel mit Hilfe von komplementär Winkeln und der innenwinkelsumme einträgst, sollte es ein leichtes sein die fehlenden Größen des kleinen Dreiecks zu bestimmen.

tan(α)=(a/2)/a

α=tan^{-1}(1/2)=26,565°

β=90--26,565=63,435°

Answer 3

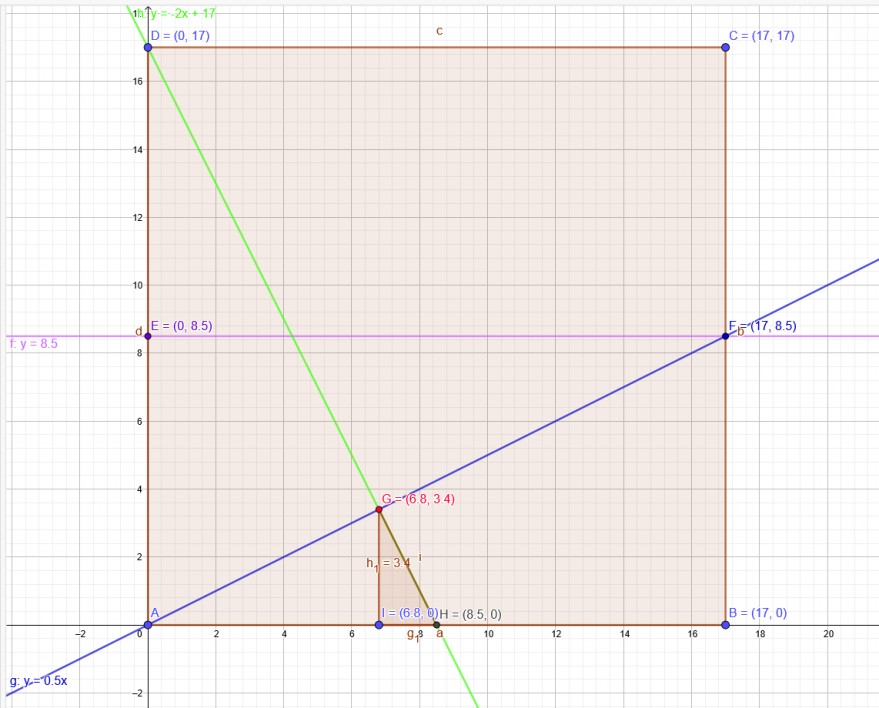
Quadrat:   A(0|0)   B(17|0)  C(17|17)  und D(0|17)

Rechteck: A(0|0)    B(17|0)  F(17|8,5)  und E(0|8,5)

Gerade durch A und F:  y=0,5x     m₁=0,5   

Orthogonale durch D mit  m₂=-2       y=-2x+17

Schnittpunkt mit y=0,5x →  G(6,8|3,4)     

Nullstelle von   y=-2x+17   → H(8,5|0)

Fläche des Trapez B F G I: \( \frac{8,5+3,4}{2} \)•(17-6,8)=60,69\( cm^{2} \)

Fläche des Dreiecks G I H: \( \frac{8,5-6,8}{2} \)•3,4=2,89\( cm^{2} \)

Gesuchte grüne Fläche:60,69\( cm^{2} \)-2,89\( cm^{2} \)=57,8\( cm^{2} \)