Kann mir jemand erklären wo mein Fehler ist?
Dein Fehler liegt darin, dass man die 'Fallunterscheidung' \(z-1\ge0\) und \(z-1\lt0\) nur machen kann, wenn \(z \in \mathbb R\) - also \(z\) eine reelle Zahl ist. Aber das ist nicht der Fall. Dein Ergebnis \(z=2-i/2\) führt direkt zu einem Widerspruch.
Zeichne Dir das mal in der Gaußschen Ebene auf:
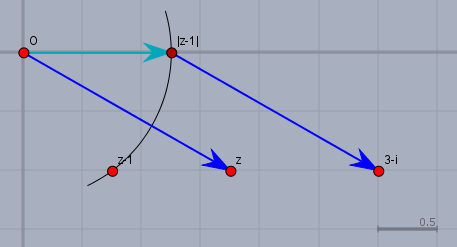
oben siehst Du die imaginären Zahlen \(3-i\), \(z\), \(z-1\) und \(|z-1|\). Die Zahl \(|z-1|\) hat keinen imaginären Anteil und befindet sich daher auf der horizontalen Achse. \(|z-1|\) hat aber den gleichen Abstand zum Ursprung \(O\) wie \(z-1\).
Die Addition von \(|z-1|\) (hellblauer Pfeil) und \(z\) (blauer Pfeil) ergibt \(3-i\).