Gut Roland Frage:
bei no 7 : wenn ich da bin, dann sehe ich SCHON den Eingang. Warum auch hier 2 Wege?
no 6 ist klar, ja
Zweite Sache : ich she EHRLICH die Lösung UNGERN im Buch, aber hier steht NUR 5!!
Stimmt es sind NUR 5?
Lösung

Text erkannt:
4. a) \( \begin{aligned} 11111 &=31 \\ 111111_{\theta} &=63 \\ 1111111_{\otimes} &=127 \end{aligned} \)
8 vierstellige Zahlen;
16 fünfstellige Zahlen
5. (1) \( 1011_{\text {Q }} \)
(2) 100101
(3) 1001001
(4) 1100
(5) 11001
(6) 10011
6. 5 -mal; \( 11111_{Q} \)
Das Zwölfersystem
Text erkannt:
5. Rechne im Zweiersystem:
(1) 110 (2)
(2) \( 11011_{\text {(2) }} \)
(3) \( 111011_{@} \)
(S)
\( \begin{array}{ll}\text { (5) } 101111_{\odot} & \text { (6) } 110001_{\text {@ }}\end{array} \)
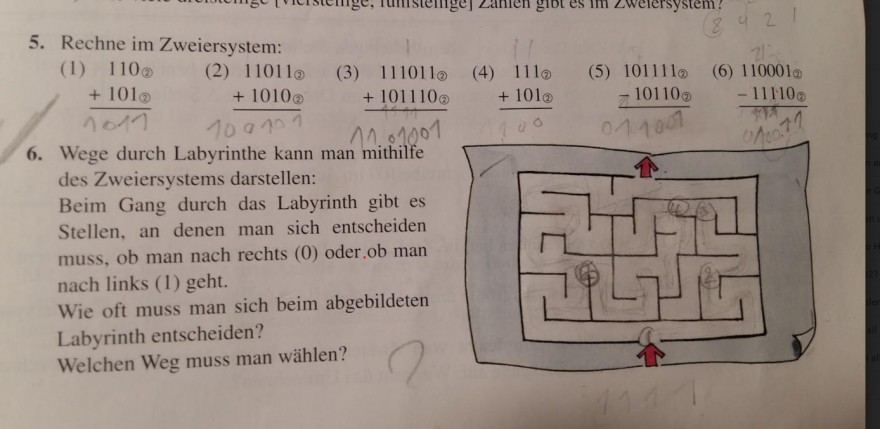
6. Wege durch Labyrinthe kann man mithilfe des Zweiersystems darstellen:
Beim Gang durch das Labyrinth gibt es Stellen, an denen man sich entscheiden muss, ob man nach rechts (0) oder.ob man nach links (1) geht.
Wie oft muss man sich beim abgebildeten Labyrinth entscheiden?
Welchen Weg muss man wählen?