Ich berechne mal die Stellen mit der Ableitung = 0
f(x):= 2cosx+sin(2x)
f '(x) = - 2 sinx + 2*cos(2x) = 0
2 cos (2x) = 2 sin x |Additionstheorem für cos(x+x)
2 (cos2 x - sin2 x) = 2 sin x |cos2 x = 1 - sin2 x
2( 1 - 2 sin2 x) = 2 sinx |:2
1 - 2 sin2 x = sin x
0 = 2 sin2 x + sinx - 1
sin x = 0.25 * (-1 ±√(1 +8)) =
sin x = 0.25 * (-1 ± 3) = 0.5 und -1
Aus + in ± folgt: x1 = 30° = Pi/6 = 0.524 RAD und x2 = 5 Pi /6 = 150° = 2.618 RAD, x3 = 1.5 Pi = 270° = 4.72 RAD
f '(x) = - 2 sinx + 2*cos(2x) = 0
f ' ' (x) = - 2 cos x - 2*2 sin (2x)
x1 und x2 einsetzen gibt nicht 0. Deshalb handelt es sich um Extremalstellen.
x3 eingesetzt gibt aber wieder 0. Durch Testen in f(x) mit 2 Werten ganz nahe bei x3 ist klar, dass die Funktion auf beiden Seiten von x3 steigt. Somit gibt's dort kein lokales Extremum. Es liegt ein Terrassenpunkt vor.
f' hat somit 3 Nullstellen im Intervall [0, 2Pi)
Die Nullstellen von f kannst du mit der Lösung der ähnlichen Aufgabe bestimmt selber finden.
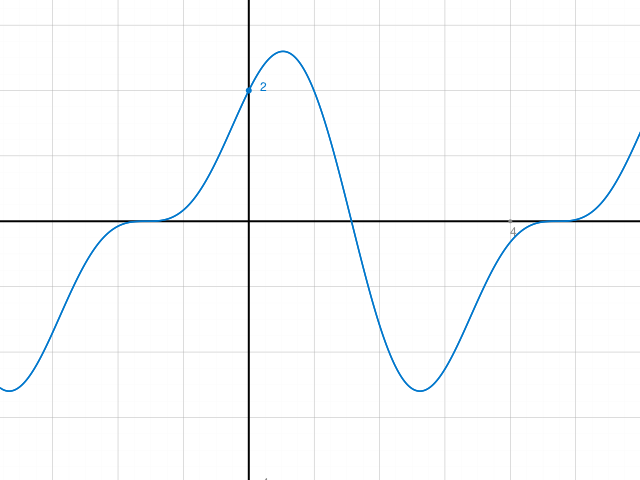
Als Kontrolle noch ein Graph von f(x):