Matrix aus Kern und Bild herleiten

Question

Aufgabe:

Konstruiere eine 4x4 Matrix A mit folgenden Eigenschaften:

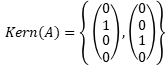
Text erkannt:

$\operatorname{Kern}(A)=\left\{\left(\begin{array}{l}0 \\ 1 \\ 0 \\ 0\end{array}\right),\left(\begin{array}{l}0 \\ 0 \\ 1 \\ 0\end{array}\right)\right\}$

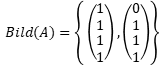
Hinweis:

Text erkannt:

$\operatorname{Bild}(A)=\left\{\left(\begin{array}{l}1 \\ 1 \\ 1 \\ 1\end{array}\right),\left(\begin{array}{l}0 \\ 1 \\ 1 \\ 1\end{array}\right)\right\}$

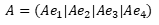
Text erkannt:

$A=\left(A e_{1}\left|A e_{2}\right| A e_{3} \mid A e_{4}\right)$

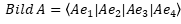
Text erkannt:

$\operatorname{Bild} A=\left\langle A e_{1}\left|A e_{2}\right| A e_{3} \mid A e_{4}\right\rangle$

Problem/Ansatz:

Wie verstehe ich diesen Hinweis?

Stimmt es das die Vektoren von Bild A 1:1 in der gesuchten Matrix existieren?

Und wie komme ich auf die Lösung? Wäre für einen Lösungsweg mit Erklärung dankbar.

vg coffee.cup

Answer 1

Wie verstehe ich diesen Hinweis?

Die Spalten der Matrix sind die Bilder der Basisvektoren.

Also sieht die Matrix so aus

1  0  0  0
1  0  0  1
1  0  0  1
1  0  0  1

Comments

die Matrix

besser : eine mögliche Matrix

Anmerkung zum Aufgabentext : Dass Mengenklammern auch Erzeugnisklammern sind ist mir neu.

---

Okay also kann man dann den Kern ignorieren?

Das mit den Klammern stand so in der Aufgabenstellung.

---

Da e2 und e3 eine Basis für den Kern

bilden, bestehen die 2. und 3. Spalte der

Matrix nur aus 0en.