Hallo,
zu 1)
Welche Länge d hat die Stange, welchen Winkel ρ bildet sie mit der x1/x2- Ebene?
Für die Länge der Stange verwendest du die Formel
\( \mathrm{d}(\mathrm{A} ; \mathrm{B})=\sqrt{\left(\mathrm{b}_{1}-\mathrm{a}_{1}\right)^{2}+\left(\mathrm{b}_{2}-\mathrm{a}_{2}\right)^{2}+\left(\mathrm{b}_{3}-\mathrm{a}_{3}\right)^{2}} \)
und für den Winkel mit der Ebene
\(sin(\alpha)=\frac{\vec{a}\circ\vec{b}}{|\vec{a}|\cdot|\vec{b}|}\),
wobei a der Richtungsvektor der Geraden durch die beiden Punkte und b der Normalenvektor der Ebene ist.
2.) Die Plane soll durch zwei ebene Glasplatten ersetzt werden, die V-förmige Dachform aber erhalten bleiben. Warum ist das mit den bisher verwendeten (sechs!) Befestigungspunkten nicht möglich?
Wenn du das Gebilde betrachtest, stellst du fest, dass die Punkte Z1, Z2, P1' und P4' nicht auf einer Ebene liegen.
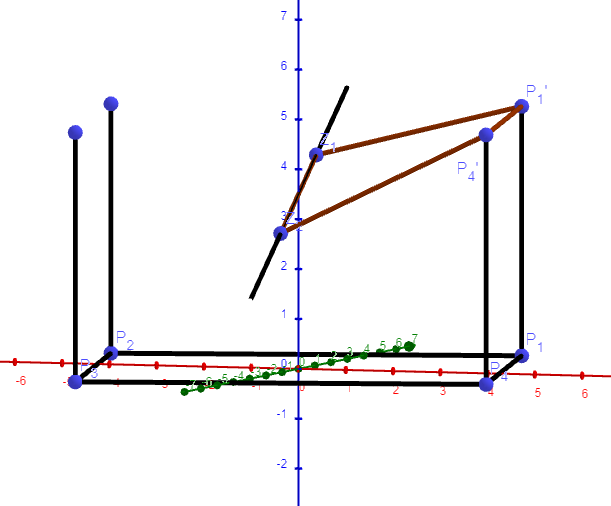
Das Gleiche gilt für die Punkte Z1, Z2, P2' und P3':

Das kann man natürlich auch rechnerisch nachweisen, aber ich belasse es jetzt bei den Skizzen.
3.) Um die Forderung laut c) zu erfüllen, muss der Architekt die Pfosten P1 und P2 erhöhen. Um welchen Betrag?
Stelle die Ebenengleichung durch die Punkte Z1, Z2 und P4' auf und setze sie gleich mit der Geraden durch P1 und P1'. Die z-Koordinate des Schnittpunktes verrät dir, um wieviel Einheiten der Pfosten verlängert werden muss (im Vergleich zu der z-Koordinate von P1).
4.) Welchen Winkel δ bilden die beiden Dachteile nun miteinander?
Der Schnittwinkel zwischen zwei Ebenen ist der spitze Winkel zwischen ihren Normalenvektoren n2 und n2:
\( \cos \angle\left(\vec{n}_{1}, \vec{n}_{2}\right)=\frac{\vec{n}_{1} \cdot \vec{n}_{2}}{\left|\vec{n}_{1}\right| \cdot\left|\vec{n}_{2}\right|} \)
Gruß, Silvia