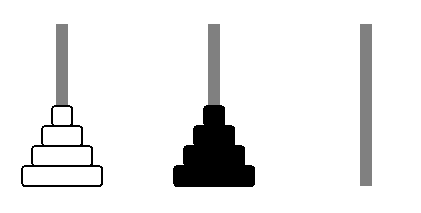
für die Uni muß ich einen rekursiven Algorithmus für ein Problem implementieren, das ähnlich den Türmen von Hanoi ist. Gegeben sind zwei gleich große Türme, es gibt drei Stäbe und Ziel ist es die Positionen der beiden Türme zu tauschen, also wo der schwarze war, soll der weiße stehen, und andersherum. Regeln sind wie beim normalen Türme von Hanoi und es dürfen gleich große Scheiben aufeinander liegen.
Die Aufgabenstellung empfiehlt als status quo einen Zwischenstand, bei dem alle Scheiben rechts mit wechselnder Farbe sind (siehe Anhänge).
Die rekursive Lösungsfunktion soll das gleiche Format haben wie die vom normalen Hanoi-Problem, also etwa moveTower( Stab from, Stab to, Zahl i, Stab temp).
Folgendes habe ich nun seit ein paar Stunden erfolglos versucht: Für n=2 und n=3 explizite Lösungen probiert und versucht einen Rekursionsbaum aufzustellen. Leider ziemlich erfolglos...
Daher wende ich mich nun an euch und hoffe, dass der ein oder andere einen hilfreichen Rat hat.
,
eman