Also ich habe zwar die Lösung von meiner freundin bekommen, jedoch schreibt sie nie den rechenweg auf... natürlich möchte ich das aber verstehen können.. und ich weiß bei der a) schon nicht, was ich da machen soll... Danke für die Hilfe im voraus!
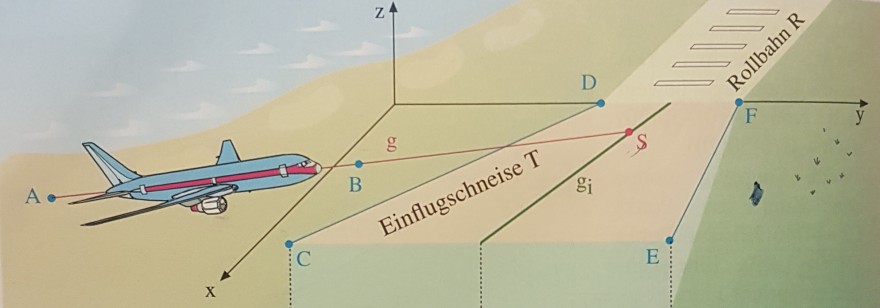
Ein Flugzeug befindet sich im Landeanflug. Es bewegt sich auf einer geraden Flugbahn g durch die Punkte \( \mathrm{A}(25|2| 5) \) und \( \mathrm{B}(15|7| 3) . \) Die Einflugschneise wird durch zwei Geraden \( \mathrm{g}_{1} \) und \( g_{2} \) begrenzt, welche durch die Punkte \( \mathrm{C}(10|4| 2) \) und \( \mathrm{D}(0|10| 0) \) bzw. \( \mathrm{E}(10|20| 2) \) und \( \mathrm{F}(0|14| 0) \) gehen (Angabe in \( \mathrm{km} \) ).
a) Bestimmen Sie die Gleichungen der beiden Begrenzungsgeraden \( g_{1} \) und \( g_{2} . \) Zeigen Sie, dass diese eine Ebene T aufspannen. Wie lautet die Gleichung der Ebene T?
b) Welchen Winkel bildet die Ebene T (Einflugschneisenebene) mit der Rollbahnebene \( R \), welche wie abgebildet in der \( x-y \)-Ebene liegt?
c) Wie lautet die Gleichung der Flugbahngeraden g des Flugzeugs?
d) Die in der Mitte der Einflugschneise verlaufende Gerade \( \mathrm{g}_{\mathrm{i}} \) ist die ideale Linie für den Landeanflug. Wie lautet die Gleichung der Geraden \( g_{i} \) ? Zeigen Sie, dass die Bahn g des Flugzeugs die Ideallinie \( \mathrm{g}_{\mathrm{i}} \) schneidet. Wo liegt der Schnittpunkt \( S ? \)
e) Berechnen Sie, um welchen Winkel der Pilot den Kurs in S korrigieren muss, um auf die Ideallinie \( \mathrm{g}_{\mathrm{i}} \) einzuschwenken.
f) Das Flugzeug hat eine Geschwindigkeit von \( 500 \frac{\mathrm{km}}{\mathrm{h}} \). Wie lange dauert der Landeanflug von Punkt A bis zum Aufsetzen am Beginn der Rollbahn?