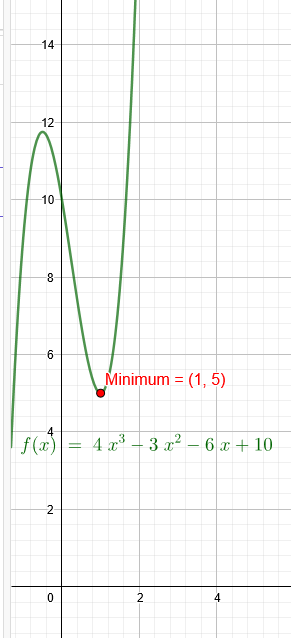
"Die kubische Polynomfunktion f mit f(x) = a\( x^{3} \) + b\( x^{2} \) − 6x + 10 hat im Punkt T = (1 | 5) ein lokales Minimum. Berechne die Koeffizienten a und b."
Weg über die Nullstellenform der kubischen Parabel:
Ich verschiebe den Graphen um 5 Einheiten nach unten: T´(1 | 0) doppelte Nullstelle
p(x)=a\( x^{3} \) + b\( x^{2} \) − 6x + 5
p(x)=a*(x-1)^2*(x-N)=a*[(x^2-2x+1)*(x-N)]=ax^3-aNx^2-2ax^2+2axN+ax-aN=
=ax^3+(-aN-2a)*x^2-(-2aN-a)*x-aN
Koeffizientenvergleich:
1.)b=-aN-2a
2.)-2aN-a=6
3.)-aN=5 →-2aN=10 in 2.)10-a=6 → a=4 in 3.) -4N=5 →N=-\( \frac{5}{4} \)
b=-4*(-\( \frac{5}{4} \))-8=-3
p(x)=4\( x^{3} \) -3\( x^{2} \) − 6x + 5
Nun wieder 5 Einheiten nach oben:
f(x)=4\( x^{3} \) -3\( x^{2} \) − 6x + 10