Grenzwert mit Konstante - l'Hospital

Question

Der folgende Grenzwert ist mit der Regel von l'Hospital zu berechnen:

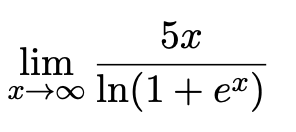
Text erkannt:

$\lim \limits_{x \rightarrow \infty} \frac{5 x}{\ln \left(1+e^{x}\right)}$

Bekomme, nach erster Ableitung von Zähler und Nenner folgendes raus:

(5) / (e^x / 1+e^x)
Der Nenner geht ja immer noch gegen unendlich, sogar exponentiell.
l'Hospital kann man auch nicht mehr anwenden, da der Zähler eine Konstante erhält. Somit müsste der Grenzwert doch 0 sein, da durch unendlich geteilt wird - aber laut Löung kommt hier die 5 raus.
Woran liegt das? Wo ist mein Fehler?

Answer 1

Aloha :)

Du kannst die Krankenhaus-Regel immer anwenden, wenn Zähler und Nenner gegen denselben Grenzwert konvergieren (bzw. gegen $\infty$ gehen). Für $x\to\infty$ gehen Zähler und Nenner gegen $\infty$. Du kannst hier also Zähler und Nenner unabhängig voneinander nach $x$ ableiten:

$$\lim\limits_{x\to\infty}\frac{5x}{\ln\left(1+e^x\right)}=\lim\limits_{x\to\infty}\frac{5}{\underbrace{\frac{1}{1+e^x}}_{\text{äußere A.}}\cdot\underbrace{e^x}_{\text{innere A.}}}=\lim\limits_{x\to\infty}\frac{5+5e^x}{e^x}=\lim\limits_{x\to\infty}\left(\frac{5}{e^x}+5\right)=5$$

Comments

Danke für die gute Antwort!

Auf den Term mit 5+5e^x ... kommt man durch erweitern im Zähler und Nenner mit (1+e^x)?

Aber wäre in deinem letzten Term dann unendlich plus 5 nicht auch unendlich? Oder hast du bei der 5/e^x noch das e^x im Zähler vergessen?

---

Ja genau, du erweiterst mit $(5+5e^x)$.

Im letzten Schritt wird die Exponentialfunktion unendlich groß. Wenn der Nenner unendlich groß wird, der Zähler aber konstant bleibt, geht der Bruch gegen $0$. Ich schreibe das mal symbolisch:$$\frac{5}{e^x}\stackrel{(x\to\infty)}{\to}\frac{5}{e^{\infty}}=\frac{5}{\infty}=0$$

---

Danke, jetzt hab ichs!

Answer 2

Ich denke, es liegt daran , dass der Nenner gegen 1 konvergiert, denn

e^x/(1+e^x)=

1/((1/e^x)+1)= Nun soll x gegen unendlich gehen

dann ist der Nenner 1/(0+1)=1/1=1

Somit konvergiert der Bruch gegen 5

Answer 3

$\frac{5 \cdot \infty }{\infty } = 5$

Comments

$\frac{5 \cdot \infty }{\infty } = 5$

Du kannst dich noch retten, wenn du sagst, dass das nur ein Scherz war.