Aufgabe:
Ich soll die folgende analoge Formel der empirischen Kovarianz zeigen:
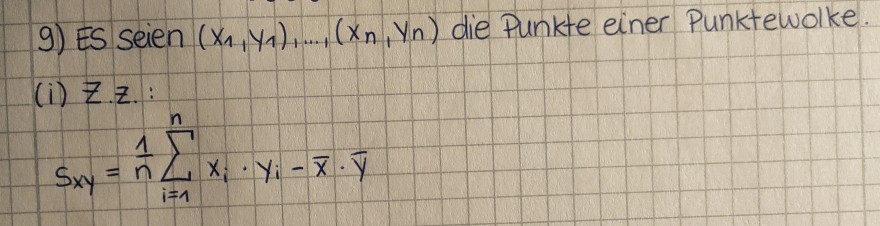
Text erkannt:
9) ES seien \( \left(x_{1}, y_{1}\right), \ldots,\left(x_{n}, y_{n}\right) \) die Punkte einer Punktewolke,
(i) Z.Z. :
\( S_{x y}=\frac{1}{n} \sum \limits_{i=1}^{n} x_{i} \cdot y_{i}-\bar{x} \cdot \bar{y} \)
Ich habe damit begonnen, die Formel der Kovarianz aufzuschreiben und auszumultiplizieren. Allerdings hänge ich etwas fest...
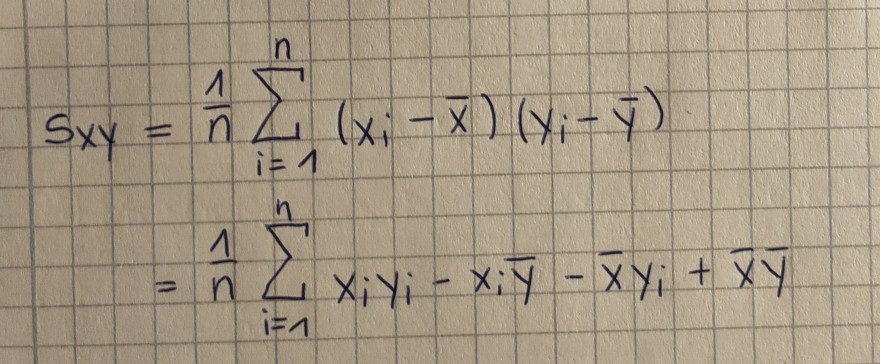
Text erkannt:
\( \begin{aligned} S_{x y} &=\frac{1}{n} \sum \limits_{i=1}^{n}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right) \\ &=\frac{1}{n} \sum \limits_{i=1}^{n} x_{i} y_{i}-x_{i} \bar{y}-\bar{x} y_{i}+\bar{x} \bar{y} \end{aligned} \)
Ich würde mich freuen, wenn mir jemand helfen könnte. :)