Hi Sophie,
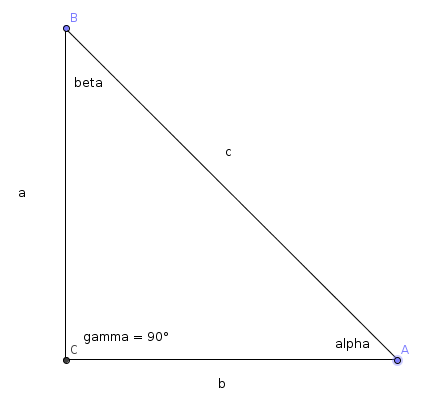
a) sin (α) = cos (β)
sin(α) = Gegenkathete/Hypotenuse = a/c
cos(β) = Ankathete/Hypotenuse = a/c
b) Die Werte von cos(α) und von sin (α) sind stets kleiner als 1
cos(α) = Ankathete/Hypotenuse; da Hypotenuse > Ankathete, folgt cos(α) < 1
Für sin(α) analog.
c) Die Werte von tan (α) können beliebig groß sein
tan(α) = Gegenkathete/Ankathete
Da man a und b beliebig verändern kann (also a beliebig groß und b beliebig klein machen kann), folgt die Aussage.
Zum Beispiel a = 1000, b = 0,01 => tan(α) = 100.000
d) Ist das Dreieck gleichschenklig, so gilt sin (α) = cos (α) = tan (α) = 1
Das sehe ich nicht :-(
Lieben Gruß
Andreas