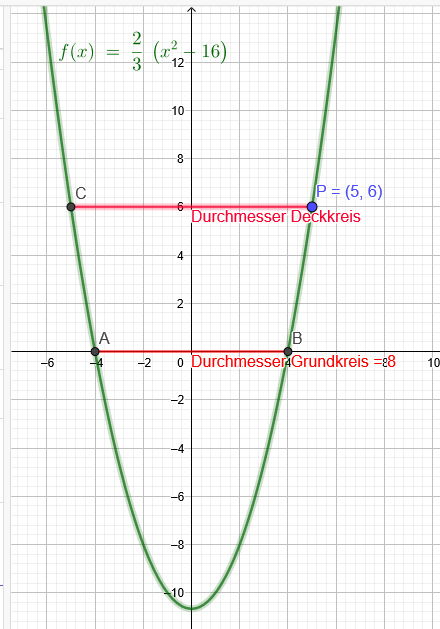
Nullstellenform der Parabel:
y=a(x-4)*(x+4)=a*(x^2-16)
P(5|6)
y(5)=a*(5^2-16)=9a
9a=6 a=\( \frac{2}{3} \)
y=\( \frac{2}{3} \)*(x^2-16)=\( \frac{2}{3} \)x^2-\( \frac{32}{3} \)
Auflösung nach x
\( \frac{2}{3} \)x^2=y+\( \frac{32}{3} \)|*\( \frac{3}{2} \)
x^2=\( \frac{3}{2} \)*y+16
x=\( (1,5*y+16)^{0,5} \)
g(y)=\( (1,5*y+16)^{0,5} \)
Volumen bei Drehung um die y-Achse:
\( V=\pi \cdot \int \limits_{0}^{6}(1,5 y+16) \cdot d y=\pi \cdot\left[0,75 y^{2}+16 y\right]_{0}^{6}=\pi \cdot[0,75 \cdot 36+16 \cdot 6]=123 \pi \)\( dm^{3} \)
2) Berechne, wie hoch darin 100 Liter Wasser stehen.
100=π*\( \int\limits_{0}^{h} \)(1,5y+16)=π*[0,75h^2+16h]
h≈1,832dm