Aufgabe: Riemann-Integral Definition und Definition uneigentliches Integral
Problem/Ansatz:
Hallo,
leider komme ich auch bei dieser Aufgabe nicht weiter... Ich verstehe nicht wie ich von der Definition des normalen Riemann Integrals auf die Definition der uneigentlichen Riemann Integrale schließen muss, bzw. deren Gleichheit zeigen soll.
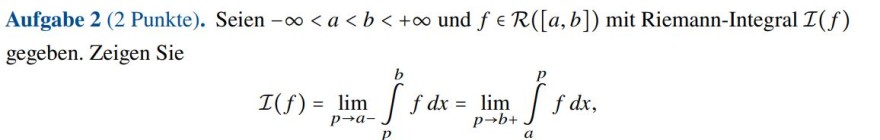
Text erkannt:
Aufgabe 2 (2 Punkte). Seien \( -\infty<a<b<+\infty \) und \( f \in \mathcal{R}([a, b]) \) mit Riemann-Integral \( \mathcal{I}(f) \) gegeben. Zeigen Sie
\( \mathcal{I}(f)=\lim \limits_{p \rightarrow a-} \int \limits_{p}^{b} f d x=\lim \limits_{p \rightarrow b+} \int \limits_{a}^{p} f d x \)
