Definition des Riemann-Integrals

Question

Liebe Lounge,

ich habe eine Frage zur Definition des Riemann-Integrals.

Und zwar möchte ich die Version mit Ober- und Untersummen verwendet.

Dort steht nun:

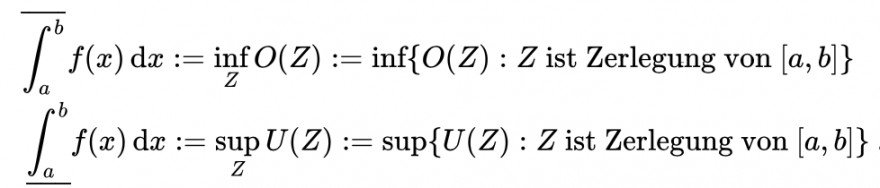
Wieso wird in dieser Definition nicht Minimum {O(z)} und Maximum {U(Z)} benutzt? Weil dadurch dass wir O(Z) und U(Z) bestimmen können, werden die Obersummen und Untersummen ja auch tatsächlich angenommen?

Ich verstehe es, weshalb Ober- und Untersummen für sich selbst so definiert sind:

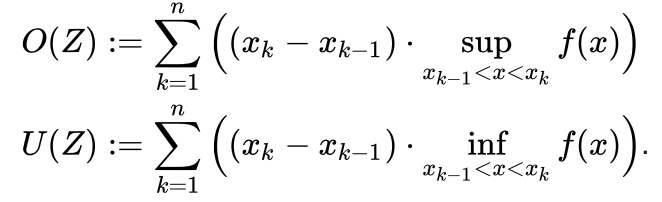
Hier ist es logisch, da bei unstetigen Funktionen Max und Minimum nicht immer angenommen werden.

Aber wieso wird es oben so definiert?

!

Answer 1

Hallo

du kannst doch nicht ALLE  O(Z) bestimmen, für alle Unterteilungen? woher kennst du dann das Min oder Max? wenn du es kennst ist ja inf=Min usw.

Gruß lul

Comments

Aber dann kenne ich doch das Infimum auch nicht ?

---

Oder ist damit gemeint, dass wenn man bspw. f(x)=x^2 integriert auf I=[0;1] dass dann ja die Untersumme gegen 1/3 konvergiert und die Obersumme auch. Allerdings wird es keine Ober- und keine Untersumme geben, die tatsächlich den Wert annimmt.

1/3 ist deshalb das Infimum und das Supremum, nicht aber Minimum und Maximum.

Richtig?