Dein Ergebnis für r ist richtig.
Das setzt du jetzt in die Geradengleichung ein:
\( \left(\begin{array}{l}2 \\ 1\end{array}\right)-\frac{24}{7} \cdot\left(\begin{array}{l}3 \\ 2\end{array}\right)= \)
\( \left(\begin{array}{l}2-3 \cdot \frac{24}{7} \\ 1-2 \cdot \frac{24}{7}\end{array}\right)= \)
\( \left(\begin{array}{l}2-\frac{72}{7} \\ 1-\frac{48}{7}\end{array}\right)= \)
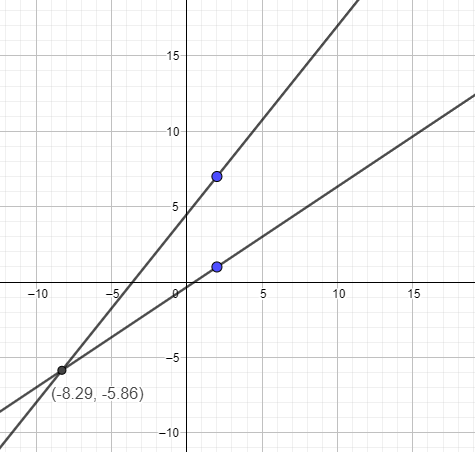
\( \left(\begin{array}{l}-\frac{58}{7} \\ -\frac{41}{7}\end{array}\right) \approx\left(\begin{array}{l}-8,29 \\ -5,86\end{array}\right) \)